Расстояние между двумя точками онлайн. Как найти расстояние между точками?

Теперь поговорим о правильном треугольнике ABC. Чтобы найти расстояние на плоскости между точкой A и точкой B, используйте формулу:

Простейшие задачи аналитической геометрии на плоскости

Например, если даны точки, то расстояние между ними равно:

Теорема 2.Для каждой точки

которые не лежат на одной прямой, площадь треугольника

Например, определим площадь треугольника, образованного точками и

Наблюдение. Если площадь треугольника равна нулю, это означает, что точки лежат на одной прямой.

Учитывая, что любой отрезок в плоскости

определяется равенством отношения, в котором находится точка .

Задача деления отрезка по заданному отношению заключается в следующем
вокруг координат точки
Теорема 3.Если точка отношения

тогда координаты точки определяются по следующей формуле: — координаты точки — координаты точки

Из этого следует:Если

где, то ).

Например. Точки заданы через, координаты точки определяются вместо.

Решение.
Из,
После прямоугольной системы координат наиболее важной является полярная система координат. Она состоит из точки с полюсом и радиуса исходящей из нее полярной оси. Кроме того, определяется единица измерения для измерения длины сегментов.

Полярная система координат и расстояние от точки

; .

является полярной координатой точки и считается первой координатой и называется полярным радиусом, числом полярного угла.

Однако в некоторых случаях нам необходимо определить углы, измеряя их по часовой стрелке от полярной оси.

Связь между полярными координатами точки и ее прямоугольными координатами.

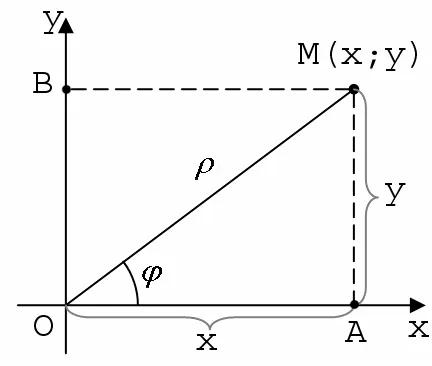
Предположим, что начало прямоугольной системы координат находится на полюсе, а положительная полуось крайнего положения совпадает с полярной осью.

Пусть — в полярной системе координат. Например. Затем

С другой стороны, согласно теореме Пифагора.

(1.6) — эти формулы выражают полярные координаты через ортогональные координаты.

Заметим, что формула для, получается после выбора точки, в которой уравнения удовлетворяются.
Например, найдите полярные координаты точки. или I квадранта.
Пример 1: Найдите точку, симметричную относительно.

Проведите через точку A прямую l₁перпендикулярно биссектрисе l первого координатного угла. Пусть l₁определить сегмент CA₁равна отрезку AC. Прямоугольные треугольники АСО и А₁CO равны между собой (через два зонда). Поэтому | OA | = | OA₁|. Треугольники ADO и OEA₁также равны друг другу (по гипотенузе и острому углу). Сделайте вывод, что |AD | = |OE| = 4, |OD| = |EA₁| = 2, т.е. точка имеет координаты x = 4, y = -2, т.е. A₁(4;-2).

Следует отметить, что существует общее утверждение: Точка A₁симметричная точке относительно биссектрис первого и третьего координатных углов, имеет координаты .

Пример 2: Найдите точку, в которой проходит прямая, проходящая через ,.

а расстояние от O до A равно x_{мы получаем:}На рисунке 2 точки A и B находятся по разные стороны от начала координат O. В этом случае расстояние между A и B одинаково:_{Поскольку координата точки A отрицательна, а координата точки B положительна, (2) можно записать в виде (2):}На рисунке 3 точки A и B лежат слева от начала координат O ._{В этом случае расстояние между A и B одинаково:}Координаты A и B отрицательны. Тогда (5) можно записать в виде (5):_{Поскольку координата точки A отрицательна, а координата точки B положительна, (2) можно записать в виде (2):}Формулы (2), (4), (6) также можно записать следующим образом:_{В этом случае расстояние между A и B одинаково:}На рисунке 2 точки A и B находятся по разные стороны от начала координат O. В этом случае расстояние между A и B одинаково:_{Поскольку координата точки A отрицательна, а координата точки B положительна, (2) можно записать в виде (2):}На рисунке 3 точки A и B лежат слева от начала координат O ._{мы получаем:}Координаты A и B отрицательны. Тогда (5) можно записать в виде (5):_{Поскольку координата точки A отрицательна, а координата точки B положительна, (2) можно записать в виде (2):}Тогда это следует из (8):

Пример 2. На плоскости, в декартовой прямоугольной системе координат XOY, точки \( \small A(x_a; \y_a)=A(-6;3)\) и \( \small B(x_b, \y_b)=B(11,-4). \) приведены. Найдите расстояние между этими точками.₁Решение. Найдите расстояние между A и B, используя формулу (9). Подставьте координаты точки A и точки B в формулу (9) и получите:₂Рассмотрим точки A и B в пространстве в декартовой прямоугольной системе координат, где A имеет координаты ( x

) и B имеет координаты ( x

) (рис. 5).

AB — диагональ параллелепипеда, грани которого параллельны координатным плоскостям и проходят через A и B. Однако AB — гипотенуза правильного треугольника AMB, а AM и BM — перпендикуляры правильного треугольника. Согласно теореме Пифагора, из этого следует:₁Решение. Найдите расстояние между A и B, используя формулу (9). Подставьте координаты точки A и точки B в формулу (9) и получите:₂.

Расстояние между двумя точками на прямой

Из предыдущего параграфа мы получаем следующее:_aНо AM=A’B’. Из (10) и (11) получаем:_b\( \small AB^2=AM^2+BM^2=A’B’^2+BM^2 \) \( \small =(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2. \)

Пример 3. Дана декартова прямоугольная система координат XOY и точки \( \small A(x_a;\y_a;\z_a)=A(5;1;0)\) и \( \small B(x_b,\y_b,\z_b)=B(-8,-4;21) в пространстве. \) Найдите расстояние между этими точками.

Решение. Найдите расстояние между A и B, используя формулу (12). Подставляя координаты A и B в формулу (12), получаем:_bОтвет:_a

Расстояние между двумя точками на плоскости

_a, y_ab, y_b

Ответ:

Расстояние между двумя точками в пространстве

_a, y_a, z_ab, y_b, z_b

Содержание раздела

• Расстояние между двумя точками онлайн
• Общее уравнение прямой на плоскости
• Каноническое уравнение прямой на плоскости
• Параметрическое уравнение прямой на плоскости
• Уравнение прямой в отрезках
• Нормальное уравнение прямой
• Отклонение точки от прямой
• Пучок прямых. Уравнение пучка прямых
• Общее уравнение плоскости
• Уравнение плоскости в отрезках
• Нормальное уравнение плоскости
• Уравнение прямой, проходящей через две точки онлайн
• Проекция точки на прямую онлайн
• Расстояние от точки до прямой онлайн
• Расстояние между прямыми на плоскости онлайн
• Расстояние между прямыми в пространстве онлайн
• Точка пересечения прямых на плоскости онлайн
• Точка пересечения прямых в пространстве онлайн
• Точка пересечения прямой и плоскости онлайн
• Линия пересечения плоскостей онлайн
• Угол между прямыми онлайн
• Угол между прямой и плоскостью онлайн
• Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости онлайн
• Уравнение плоскости онлайн
• Проекция точки на плоскость онлайн
• Расстояние от точки до плоскости онлайн
• Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости онлайн
• Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн
• Уравнение плоскости, проходящей через точку и прямую онлайн
• Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн
• Уравнение плоскости, проходящей через прямую перпендикулярно заданной плоскости онлайн
• Расстояние между плоскостями. Онлайн калькулятор
• Угол между плоскостями. Онлайн калькулятор