Во-первых, квадрат \( 10\) раз \( 10\) состоит из \( 100\) клеток. Поэтому \( 0.05\) — это \( 5\) квадратов \( 100\), \( 0.4\) — это \( 40\) квадратов \( 100\) и так далее.
Деление десятичных дробей: правила, примеры, решения
В этой статье мы рассмотрим такую важную операцию с десятичными дробями, как деление. Сначала мы изложим общие принципы, а затем объясним, как правильно выполнять деление десятичных чисел столбиками, как для других дробей, так и для натуральных чисел. Далее мы рассмотрим деление дробей на десятичные дроби и наоборот, и, наконец, покажем, как правильно делить дроби, оканчивающиеся на 0, 1, 0, 01, 100, 10 и так далее.
Здесь мы будем иметь дело только с положительными дробями. Если перед дробью стоит знак минус, необходимо научиться делить логические и действительные числа.
Основы деления десятичных дробей
Все десятичные дроби, будь то конечные или периодические, являются лишь особой формой дробей. Поэтому к ним применяются те же принципы, что и к их обычным аналогам. Таким образом, мы сводим весь процесс деления десятичных чисел к обыкновенной дроби, а затем вычисляем с помощью уже известных нам средств. Давайте рассмотрим конкретный пример.
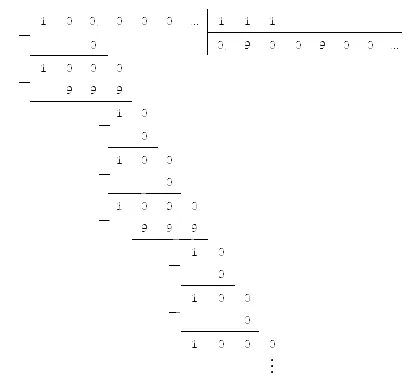
Однако, когда мы сталкиваемся с непериодическими десятичными числами в примере деления, мы действуем немного иначе. Мы не можем разделить их на обычные дроби, поэтому при делении их нужно сначала округлить до определенной цифры. Это необходимо сделать как с делителем, так и с делимым: существующая конечная или периодическая дробь также округляется для обеспечения точности.
Как разделить столбиком одну десятичную дробь на другую
Такое деление можно свести к уже описанной выше процедуре нахождения коэффициента десятичного числа и натурального числа. Нужно умножить делимое и делитель на 10, 100 и т.д., чтобы делитель стал натуральным числом. Затем выполните последовательность действий, описанную выше. Такой подход возможен благодаря свойствам деления и умножения. Мы записали их в алфавитном порядке следующим образом:
a : b = (a — 10) : ( b — 10 ), a : b = ( a — 100 ) : ( b — 100 ) и так далее.
Описанный метод позволяет разделить натуральное число на конечное десятичное число. Давайте посмотрим, как это делается.
Как делить десятичные дроби?
Деление десятичных дробей сводится к делению обыкновенных дробей. Внимательнее изучите основные правила деления десятичных чисел.
Помните, что натуральные числа — это числа, которые мы используем в повседневной жизни для счета (1, 2, 3, 4 и т.д.). Алгоритм деления натурального числа на десятичную дробь в столбик выглядит следующим образом:
- Избавляемся от запятой путем добавления к натуральному числу, столько нулей, сколько цифр после запятой в десятичной дроби;
- Выполняем обычное деление в столбик.
Чтобы разделить десятичное число на натуральное число, используйте стандартный алгоритм деления в столбик.
Пример 1: Разделите 100 на 2,5.
Согласно приведенному выше алгоритму, запятая является
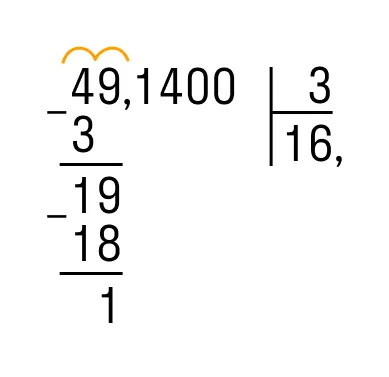
Выполните вычисления в соответствии с алгоритмом деления натурального числа на десятичную дробь, не обращая внимания на символы (чтобы избежать путаницы, символы можно опустить):
Таким образом, исходя из правила, что плюс делится на минус, в результате получается минус:
Ответ: 100 : (-2,5) = -40

Деление двух десятичных чисел сводится к предыдущему алгоритму, т.е. запятые нужно убрать. Если делитель имеет больше десятичных знаков, чем дивиденд, то к дивиденду необходимо добавить соответствующее количество нулей.
Пример 5: Разделите 12,6 на 1,12.
Поскольку делитель (1.12) имеет два знака после запятой, к делителю (12.6) нужно добавить нули, чтобы избавиться от запятых, таким образом

Ответ: 12,6 : 1,12 = 11,25
Как делить десятичную дробь на целое число?
В этом посте мы рассмотрим, как разделить десятичную дробь на целое натуральное число или другую десятичную дробь. Мы также рассмотрим примеры для закрепления представленного материала.
- Производим вычисления аналогично натуральным числам;
- В случае если присутствует знак следуем следующим правилам:
- Минус разделить на минус получится плюс;
- Минус разделить на плюс получится минус;
- Плюс разделить на минус получится минус.
- В ответе ставим нужный знак.
Чтобы разделить десятичное число на натуральное число 10, 100, 1000, 10000 и т.д., нужно сдвинуть десятичный разделитель (запятую) влево на столько мест, сколько нулей содержит делитель.
Пример 1

Пояснение: В числе 10 есть только один ноль, поэтому переместите десятичную точку на одно место влево.
Пример 2
Деление двух десятичных дробей
154,39 : 100 = 1,5439
Пояснение: Число 100 содержит два нуля, поэтому мы сдвигаем десятичную точку на одно место влево.
Примечание: Если количество нулей на линии деления превышает количество цифр в целой части делимого, отсчитайте столько цифр, сколько позволяет дробь, добавьте оставшееся количество нулей слева, поставьте запятую и добавьте ноль к целой части нового десятичного числа.

Пример 3
Деление десятичных дробей: правила, примеры
62,75 : 1000 = 0,06275
Делитель – 10, 100, 1000, 10000 и т.д.
Пояснение: Поскольку 1000 содержит три нуля, отсчитайте два места слева, прибавьте оставшийся ноль слева, поставьте запятую и запишите ноль в целой части получившейся дроби.
Разделите десятичное число на любое натуральное целое число:
Пример 4: Разделите дробь 12,516 на 3.
Пример 5: Разделите дробь 3,726 на 15.
Поскольку целая часть исходной дроби меньше делителя, это означает, что целая часть дроби равна 0 (т.е. напишите ноль, поставьте запятую и продолжайте делить).
Чтобы разделить одну десятичную дробь на другую, умножьте обе дроби на такое число (10, 100, 1000 и т.д.), чтобы они стали целыми числами (количество нулей в дроби зависит от наибольшего количества десятичных знаков в одной или другой дроби). Затем найдите коэффициент.
Примечание: Этот же прием можно использовать для деления десятичной дроби на целое число.
Пример 6: Найдите дробь 5,468 d
Делитель – любое число
- Не обращая внимания на запятую, выполняем деление столбиком, как будто делимым является целое число, а не дробь.
- Как только остаток не будет делиться нацело на делитель, ставим запятую в частном. При этом, если целая часть делимого изначально меньше делителя, значит целая часть новой дроби (частного) будет меньше единицы, т.е. равна 0.
- Продолжаем выполнять деление, записывая получаемые цифры уже в дробной части результата. Здесь, если остаток невозможно нацело поделить на делитель, к нему и к частному одновременно добавляем ноль справа и продолжаем действие до тех пор, пока не получим нулевой остаток (для конечных дробей), либо пока не будет получено требуемое количество цифр после запятой в частном.
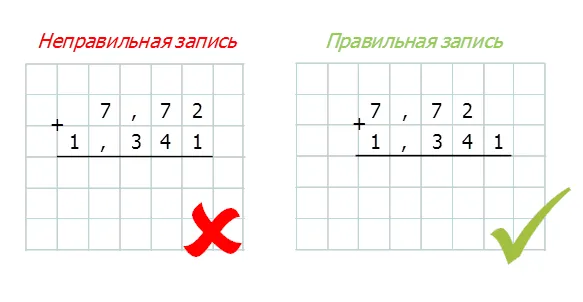
Деление десятичной дроби на другую десятичную дробь

Публикации по теме:
- Факториал числа
- Показатель степени: определение и свойства
- Таблица логарифмов
- Числа Фибоначчи
- Число Эйлера (e)
- Решение квадратных уравнений
- Определение логарифма, его свойства и график
- Натуральный логарифм числа
- Теорема Виета: для квадратного/кубического уравнения, обратная
- Степени натуральных чисел
- Факториалы натуральных чисел
- Формулы сокращенного умножения
- Арифметическая прогрессия: определение, формулы, свойства
- Геометрическая прогрессия: определение, формулы, свойства
- Производная функции: правила и формулы дифференцирования
- Нахождение производной степенной функции
- Десятичный логарифм числа
- Основное логарифмическое тождество
- Логарифм произведения (сумма логарифмов)
- Логарифм деления (частного) или разность логарифмов
- Логарифм степени (коэффициент перед логарифмом)
- Логарифмическая функция
- Решение логарифмических неравенств
- Квадрат суммы: формула и примеры
- Квадрат разности: формула и примеры
- Разность квадратов: формула и примеры
- Куб суммы: формула и примеры
- Куб разности: формула и примеры
- Разность кубов: формула и примеры
- Великая теорема Ферма
- Малая теорема Ферма
- Обыкновенные (простые) дроби
- Правильные, неправильные и смешанные дроби
- Правила сравнения обыкновенных дробей
- Приведение дробей к общему знаменателю
- Нахождение наименьшего общего кратного
- Нахождение наибольшего общего делителя
- Основное свойство дроби
- Сложение обыкновенных дробей
- Вычитание обыкновенных дробей
- Умножение обыкновенных дробей
- Деление обыкновенных дробей
- Деление числа на обыкновенную дробь
- Нахождение дроби от числа и наоборот
- Понятие десятичной дроби
- Перевод обыкновенной дроби в десятичную
- Умножение десятичных дробей: правила, примеры
- Деление десятичной дроби на обыкновенную и наоборот
- Деление натурального числа на десятичную дробь
- Умножение обыкновенной дроби на десятичную: правило, примеры








