На данном этапе полезно знать характеристики, которые позволяют классифицировать геометрическое тело как параллелограмм. К ним относятся следующие:
Как найти площадь параллелограмма
На этой странице вы можете вычислить площадь параллелограмма с помощью калькулятора с тремя формулами. Просто введите известные вам данные — площадь основания, высоту, стороны, диагонали и углы между ними — и вы получите ответ.
Параллелограмм — это четырехугольник, противоположные стороны которого попарно параллельны (лежат на параллельных прямых).
Через основание и высоту
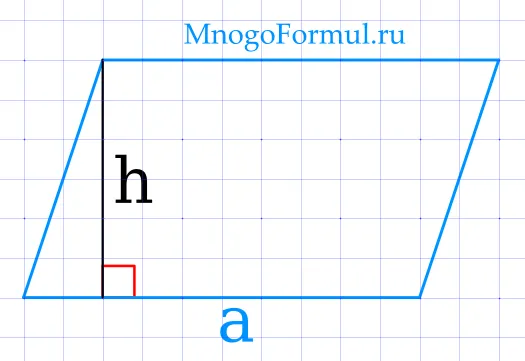
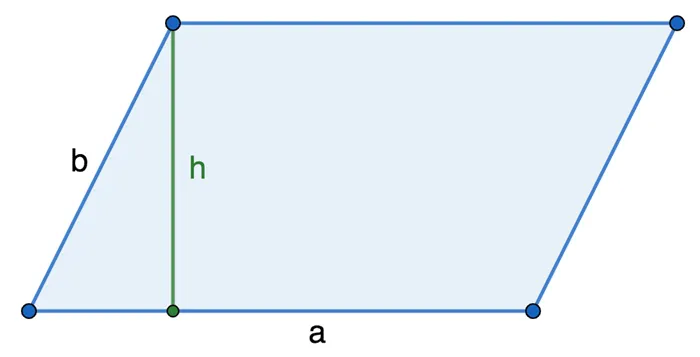
Формула для нахождения площади параллелограмма по основанию и высоте:
Где a — основание параллелограмма, а h — высота параллелограмма относительно основания.
Через стороны и угол между ними
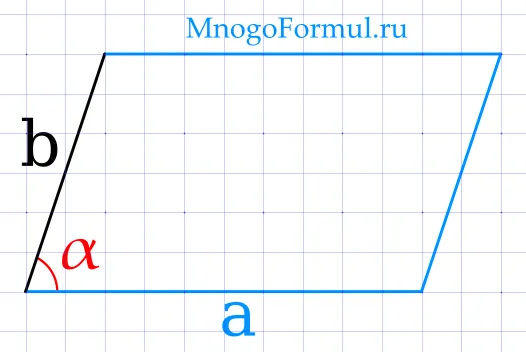
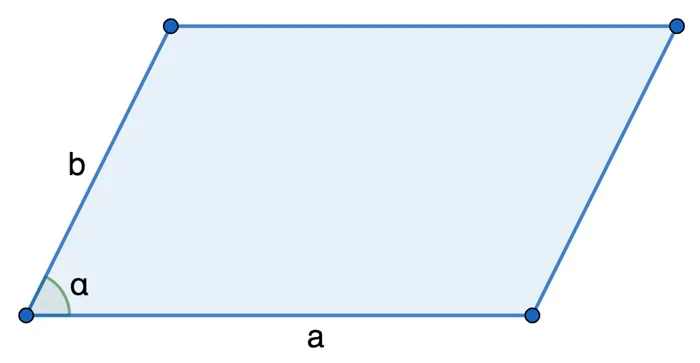
Формула для определения площади параллелограмма в терминах сторон и угла между ними:
)>Где a и b — стороны параллелограмма, а a — угол между сторонами.
Как найти площадь параллелограмма — три основных формулы
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта статья посвящена другой математической теме. Мы расскажем вам, как правильно вычислить площадь параллелограмма. Эта тема углубленно изучается только в 8 классе. И там говорится, что это не так просто.

Но сначала давайте еще раз напомним вам, какой формы параллелограмм.
Параллелограмм — это тип четырехугольника, у которого противоположные стороны параллельны друг другу.
Классический параллелограмм выглядит следующим образом:
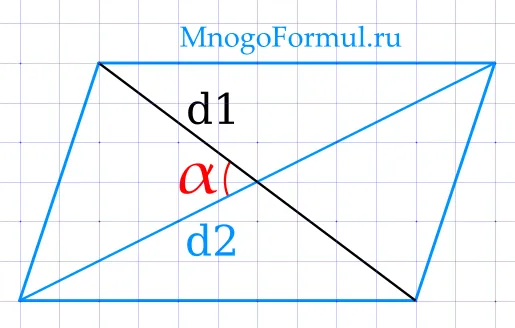
Древнегреческий математик Евклид впервые подробно описал эту форму в своем знаменитом труде «Элементы». Он также рассказал нам о двух особых случаях параллелограмма, которые мы знаем сегодня.
Это прямоугольник, у которого противоположные стороны не только параллельны, но и пересекаются под прямым углом. И квадрат, где не только противоположные стороны параллельны, но и все стороны имеют одинаковую длину.
Наконец, помните, что означает термин «площадь».
Площадь геометрической фигуры — это размер области, которая лежит в пределах сторон фигуры.
Теперь давайте объединим эти два понятия и объясним, как вычислить площадь параллелограмма.
Формулы для расчета площади параллелограмма
Существует три основные формулы для вычисления площади параллелограмма:
- если известна длина стороны и высота, проведенная к ней;
- если известны длины сторон и углы между ними;
- если известны длины диагоналей и угол между ними.
Теперь давайте рассмотрим каждый из них подробнее.
Как найти площадь параллелограмма, если известны сторона и высота
В качестве примера возьмем этот прямоугольник:
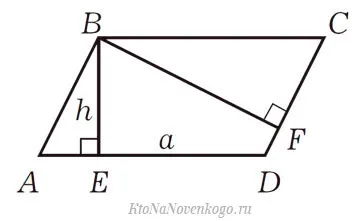
Она имеет две высоты, BE и BF, а высота — это отрезок, идущий от вершины к противоположной стороне под прямым углом.
В этом случае площадь очень легко вычислить. Вам нужно только перемножить длину высоты и длину стороны, на которой она нарисована.
То же самое можно сделать, если известны длины сторон DC и высота BF. Затем их нужно только перемножить, чтобы вычислить площадь.
Кстати, у этой формулы есть очень интересное доказательство. Поскольку противоположные стороны параллелограмма параллельны и равны, b
Наша окончательная формула для расчета площади выглядит следующим образом:
Формула площади параллелограмма, если известны стороны и угол
wikiHow работает по принципу вики, что означает, что многие наши статьи написаны более чем одним автором. Когда эта статья была создана, над ее редактированием и улучшением работали 9 человек, в том числе анонимно.

Количество просмотров этой статьи: 8667.
Параллелограмм определяется как простой четырехугольник с двумя парами параллельных сторон. Если вы увлекаетесь геометрией, вам может понадобиться определить площадь параллелограмма. Вот несколько советов о том, как именно это сделать.
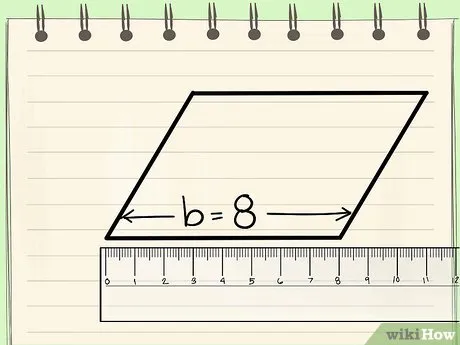
Найдите основание параллелограмма. Основание — это длина нижней стороны прямоугольника.
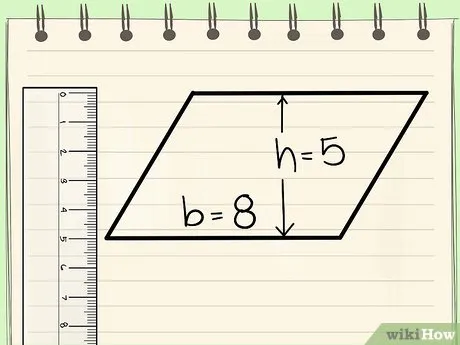
Найдите высоту прямоугольника. Высота параллелограмма — это перпендикуляр, проведенный из любой точки верхней части параллелограмма в нижнюю.
Как найти площадь параллелограмма
wikiHow основан на вики, а это значит, что многие наши статьи написаны более чем одним автором. Эта статья была отредактирована и улучшена 9 людьми, также анонимно. Количество просмотров этой статьи: 8667.
866767. Если вы продолжаете пользоваться нашим сайтом, вы соглашаетесь с нашей политикой использования файлов cookie.
Параллелограмм — это геометрическая фигура; четырехугольник, противоположные стороны которого равны и параллельны.
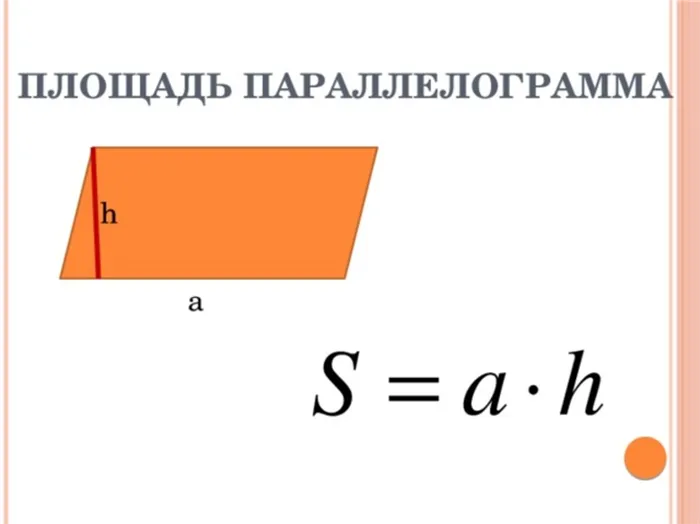
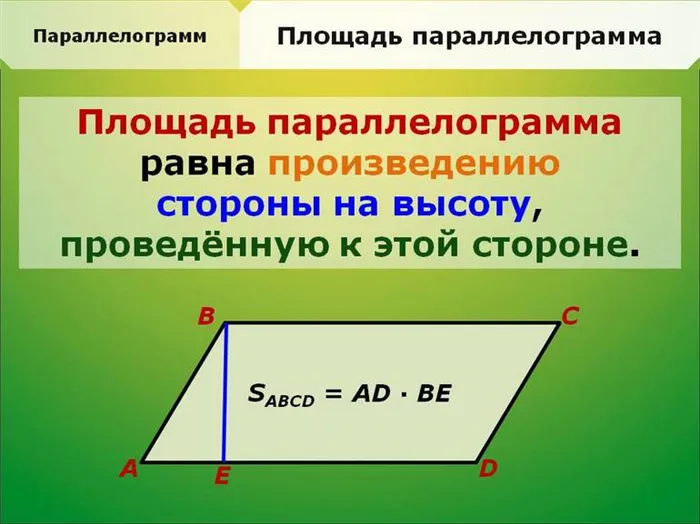
Площадь параллелограмма (S) равна произведению длины его стороны и высоты, проведенной на ней:
S = a ⋅ h
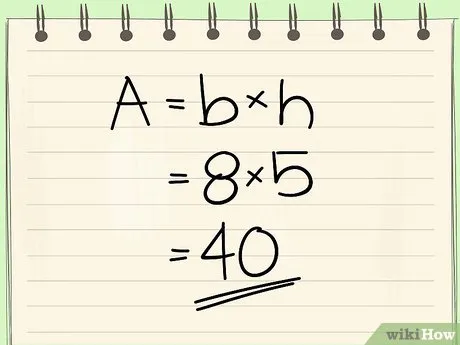
Дополнительные статьи

Об этой статье
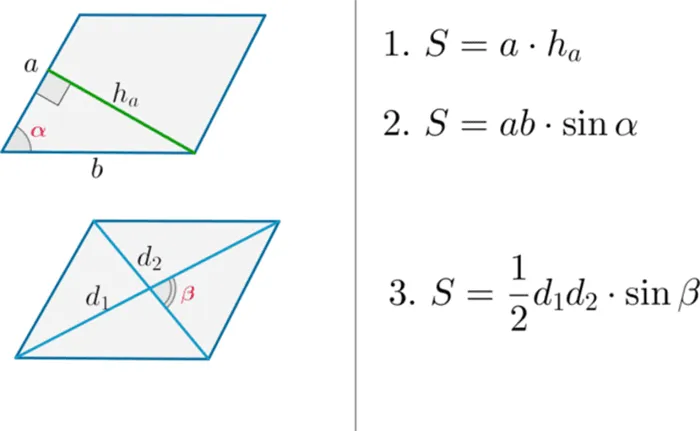
Площадь параллелограмма получается путем умножения длин двух сторон и синуса угла между ними:
S = a ⋅ b ⋅ sin a
Нахождение площади параллелограмма: формула и примеры
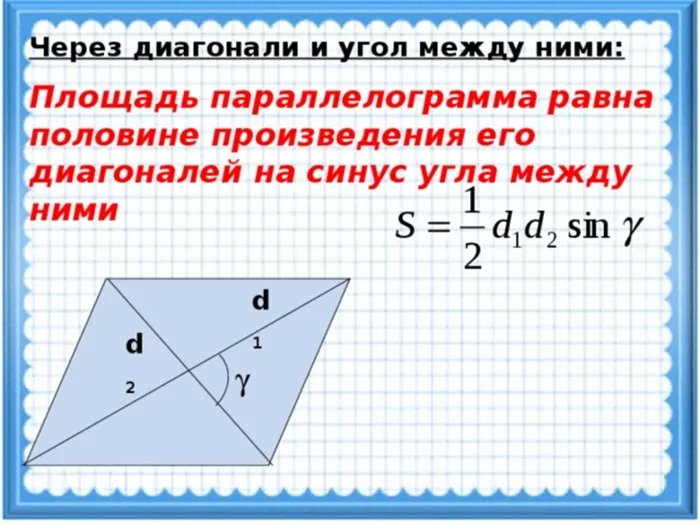
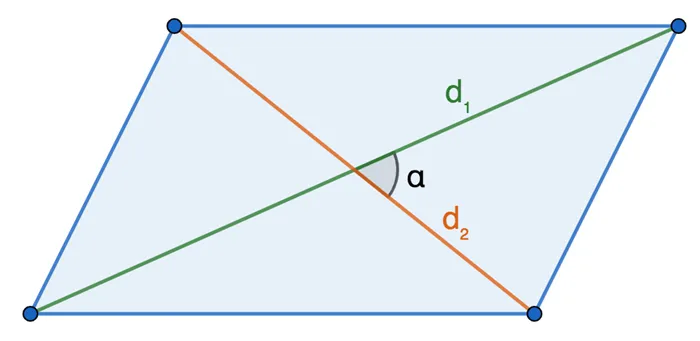
Площадь параллелограмма равна произведению одной шестой части длины его диагоналей, умноженной на синус угла между ними:
По длине стороны и высоте
Задача 1 Найдите площадь прямоугольника, если длина стороны равна 7 см, а высота — 4 см.
Решение.
По двум сторонам и углу между ними
Задача 2 Найдите площадь прямоугольника, если длина его сторон равна 6 и 8 см, а угол между ними равен 30°.
Решение.
По двум диагоналям и углу между ними
Задача 3 Найдите площадь прямоугольника, диагонали которого равны 4 и 6 см. Угол между ними равен 90°.
Примеры задач
Решение.
Публикации по теме:
- Нахождение площади квадрата: формула и примеры
- Нахождение площади прямоугольника: формула и пример
- Нахождение площади треугольника: формула и примеры
- Нахождение площади выпуклого четырехугольника: формула и пример
- Нахождение периметра квадрата: формула и задачи
- Нахождение длины окружности: формула и задачи
- Теорема Пифагора для прямоугольного треугольника: формула и задачи
- Теорема косинусов для треугольника: формула и задачи
- Тригонометрические функции острого угла в прямоугольном треугольнике
- Нахождение объема конуса: формула и задачи
- Нахождение объема тетраэдра: формула и задачи
- Нахождение объема призмы: формула и задачи
- Нахождение площади поверхности конуса: формула и задачи
- Нахождение площади поверхности шара (сферы): формула и задачи
- Нахождение площади поверхности вписанного в цилиндр шара
- Теорема Чевы: формулировка и пример с решением
- Теорема Стюарта: формулировка и пример с решением
- Теорема о трех перпендикулярах
- Признаки равенства треугольников
- Признаки подобия треугольников
- Признаки равенства прямоугольных треугольников
- Определение и свойства медианы треугольника
- Определение и свойства медианы прямоугольного треугольника
- Определение и свойства медианы в равнобедренном треугольнике
- Свойства биссектрисы равностороннего треугольника
- Нахождение радиуса вписанной в треугольник окружности
- Что такое квадрат: определение и свойства
- Нахождение радиуса вписанной в квадрат окружности
- Что такое прямоугольник: определение, свойства, признаки, формулы
- Нахождение площади сектора круга
- Нахождение длины дуги сектора круга
- Нахождение высоты трапеции: формулы и примеры задач
- Нахождение высоты равнобедренной (равнобокой) трапеции
- Нахождение высоты прямоугольной трапеции
- Что такое средняя линия четырехугольника
- Нахождение радиуса описанной вокруг куба сферы (шара)
- Нахождение радиуса вписанного в куб шара
- Нахождение площади шарового сектора
- Нахождение объема шарового сектора
- Нахождение площади шарового слоя
- Нахождение объема усеченного конуса
- Что такое цилиндр: определение, элементы, виды, варианты сечения
- Что такое пирамида: определение, элементы, виды, варианты сечения
- Что такое призма: определение, элементы, виды, варианты сечения
- Основные свойства призмы
- Нахождение радиуса вписанного в цилиндр шара (сферы)
- Нахождение радиуса шара (сферы), вписанного в правильную пирамиду
- Нахождение радиуса сферы (шара), описанной около правильной пирамиды
- Что такое правильный многоугольник: определение, признаки, элементы, виды
- Что такое ломанная: определение, обозначение, элементы, виды, пример задачи








