В греческом языке термин «parallelos» переводится как «рядом друг с другом» или «бок о бок». Этот термин использовался в древней школе Пифагора еще до того, как были определены параллельные прямые. Согласно историческим фактам, Евклид раскрыл понятие параллельных прямых в своих трудах в $III$ до н.э.
Определение параллельности прямых
Начнем с самого важного — определим, какие прямые являются параллельными в соответствии с евклидовой геометрией. Мы не зря сослались на Евклида, ведь именно в его трудах, написанных за 300 лет до нашей эры, впервые встречается упоминание о параллелизме.
Параллельные прямые определяются как прямые в одной плоскости, которые не имеют точек пересечения, даже если они продолжаются бесконечно. Они называются следующим образом.
Это кажется довольно простым, но со времен Евклида лучшие умы спорили об определении параллельных прямых и характеристиках параллельности прямых. Особый интерес представляет 5-я аксиома древнегреческого математика: Через точку, не связанную с прямой в одной плоскости, может проходить только прямая, параллельная первой. В 19 веке русскому математику Н. Лобачевскому удалось опровергнуть аксиому и указать условия, при которых через точку могут проходить по крайней мере две параллельные прямые.
Однако, поскольку учебный план ограничен евклидовой геометрией, мы принимаем вышеприведенное утверждение как аксиому.
На плоскости через любую точку, не являющуюся частью прямой, можно провести простую прямую, параллельную ей.
Уроки математики в онлайн-школе Skysmart помогут вам улучшить оценки и подготовиться к тестам, IEP и экзаменам.
Узнайте, какие предметы вызывают у вас трудности, и решайте их без заучивания формул и скучных лекций.

Свойства и признаки параллельных прямых
Существует ряд точек, по которым можно определить, параллельна ли одна прямая другой. К счастью, свойства и параллельные точки прямых тесно связаны между собой, поэтому вам не придется запоминать много информации.
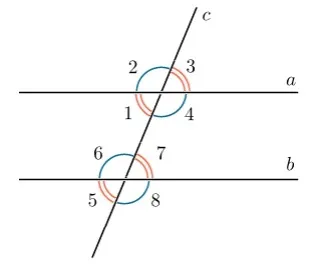
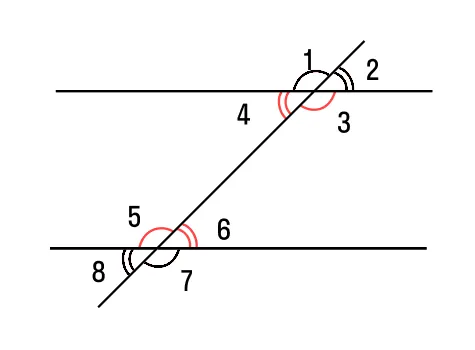
Давайте начнем со свойств. Для этого мы проводим третью линию, которая пересекает параллельные линии — она называется вспомогательной линией. В результате получается 8 углов.
Если вторичная окружность проходит через две параллельные прямые, то :
- два внутренних односторонних угла образуют в сумме 180°: ∠4 + ∠5 = 180°; ∠3 + ∠6 = 180°.
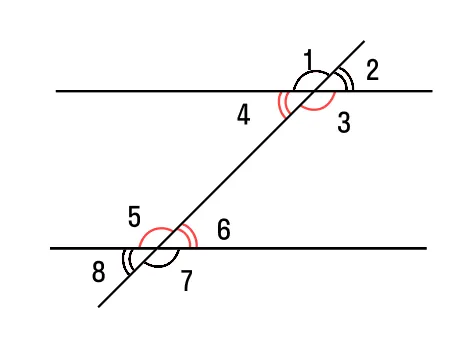
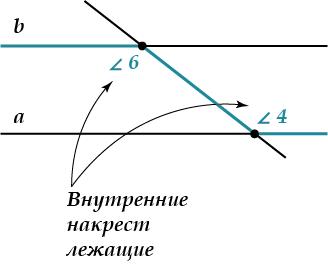
- два внутренних накрест лежащих угла равны между собой: ∠3 = ∠5, ∠4 = ∠6.

- два соответственных угла равны между собой: ∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Если вторичная прямая образует перпендикуляр к одной из параллельных прямых, то она также перпендикулярна и к другой.
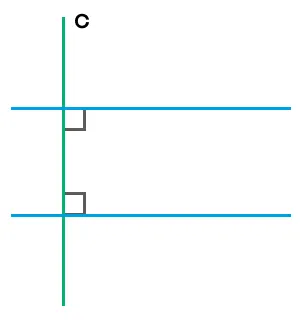
Вышеуказанные свойства также являются точками, из которых мы можем вывести параллельность прямых. Более того, достаточно установить и доказать только один пункт — остальные будут связаны с ним.
Теперь давайте посмотрим, как все эти свойства помогают нам решать задачи и практиковаться в определении параллельности двух прямых.
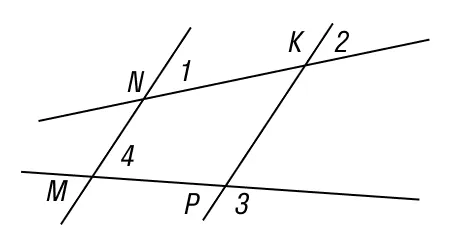
Задача 1
Линии MN и KP пересекают две другие линии и образуют разные углы. Известно, что ∠1 = 73°, ∠3 = 92°, ∠2 = 73°. Найдите значение ∠4.
Решение
В данном случае ∠3 и ∠MPK перпендикулярны друг другу, поэтому ∠MPK = ∠3 = 92°.
Поскольку ∠1 и ∠2 равны, то из их равенства следует, что MN II KP .
Согласно другому свойству параллельных прямых, ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые a и b находятся на расстоянии 27 см друг от друга. Меньшая из этих линий образует угол 150° с одной из двух линий. Найдите величину пропорции a между a и b.
Решение
Поэтому, поскольку a II b, ∠MKD + ∠KDN = 180°.
Поэтому ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM — это расстояние между прямыми a и b, поэтому DM ┴ b и наш треугольник ортогонален.
Поскольку пробник находится напротив угла 30° ½ гипотенузы, DM = 1/2DK.
DK = 2DM = 2 x 27 = 54 (см)
Что такое параллельные прямые
Параллельные прямые — это прямые, которые не пересекаются.
Это определение параллельных прямых содержит небольшую неточность: прямые, имеющие более одной общей точки, совпадают. Иногда их также называют параллельными.
Линия, которая пересекается с параллельными линиями, называется вторичной линией. Линии, пересекающиеся друг с другом, образуют 8 углов. По отношению друг к другу они могут соответствовать, быть односторонними и пересекаться. Давайте рассмотрим их для примера.
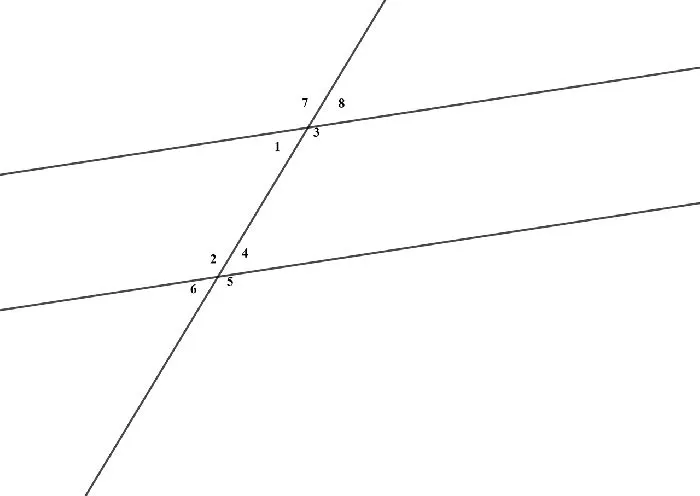
- Соответственные углы: 7 и 2, 1 и 6, 8 и 4, 3 и 5
- Накрест лежащие: 7 и 5, 8 и 6, 1и 4, 3 и 2
- Односторонние: 1и 2, 3 и 4, 7 и 6, 8 и 5
Аксиома параллельных прямых
Аксиома о параллельных прямых является одним из основных положений геометрии. Через одну точку и только через одну точку можно провести прямую, параллельную данной точке — это наиболее распространенная формулировка аксиомы.
Из этой аксиомы следуют два следствия:
- Если прямая параллельна одной из двух параллельных прямых, то она параллельна и второй.
- Если прямая пересекает одну из параллельных прямых, то она пересечет и вторую.
Обратите внимание, что аксиома применима только к плоскости. В пространстве, если прямая параллельна плоскости, возможен вариант, при котором существует бесконечное множество параллельных прямых, проходящих через одну точку. Так что в космосе это условие не обязательно выполняется.
Расстояние между параллельными прямыми одинаково в каждой точке и равно величине отрезка, перпендикулярного каждой из прямых.
Фигуры с параллельными прямыми
Существует множество фигур, в построении которых используются параллельные линии. Например, параллелограмм состоит из двух попарно параллельных отрезков.
Квадрат и прямоугольник также состоят из пар параллельных прямых, но являются частным случаем параллелограмма.
В треугольнике средняя линия всегда параллельна основанию.
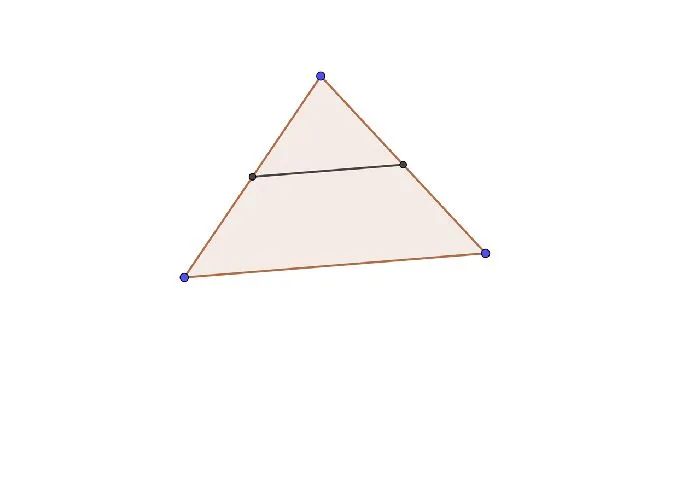
Рисунок 2: Центральная линия треугольника.
Есть еще одна интересная форма: трапеция. В трапеции большое и малое основания параллельны друг другу, а боковые стороны — нет.
Если прямые не параллельны, они пересекаются, но если отрезки не параллельны, это не значит, что они пересекаются. Сегменты имеют конечное значение длины, поэтому они могут просто отстоять друг от друга. Однако не существует отдельных типов или таблиц параллельных линий, и они вряд ли когда-либо возникнут.
Типы углов при параллельных прямых
Когда прямая пересекает две другие прямые, параллельные друг другу, образуется восемь углов. В геометрии они имеют свои названия и свойства. Чтобы углубиться в тему этой статьи, достаточно разобраться в трех типах. Затем обратитесь к рисунку ниже, рассматривая каждую точку:
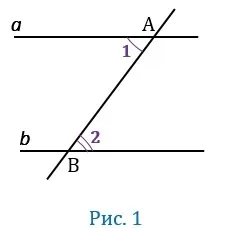
Односторонние
На рисунке выше это ∠1 и ∠6 и ∠4 и ∠7. Они находятся на одной стороне по отношению к линиям.
Соответственные
Углы 2 и 6, 3 и 7, 1 и 5, 4 и 8. Их расположение отличается тем, что они разделены прямой линией.
Накрест лежащие
На этом рисунке это ∠3 и ∠5, ∠2 и ∠8, ∠1 и ∠7, ∠4 и ∠6. Их расположение легко запомнить, потому что они расположены крест-накрест.
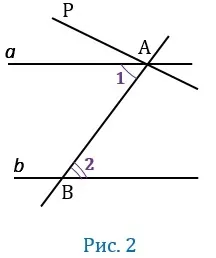
Условия параллельности
Для определения t
Накрест лежащие углы равны
Решение: \(\угол NMC=\угол DAC\) (в зависимости от ситуации) и \(\угол DAC=\угол BAD\) (AD — биссектриса угла). Поэтому \(угол NMC=\угол BAD\) .
Сумма ∠1 и ∠2 равна 180º.
a \(\vert\) b, поэтому ∠1=∠3 (соответственно). ∠2+∠3=180º (смежные). Если сложить их вместе, то получится 180º.
Это также называется теоремой о трех параллельных прямых на плоскости. Если a есть \(\vert\vert\) b и c есть \(\vert\vert\vert\) b, то a есть \(\vert\vert\vert\) c.
Соответственные углы равны
Существует \(\vert) b. Предположим, что существует еще одно c \(\vert\vert\) a. По условию, a не пересекает b и наоборот.

Здесь действует то же самое, что и в предыдущем пункте: если a и c || и b и c также ||, то a и b также ||.
Обозначение перпендикулярных линий: ⊥.
Сумма односторонних углов равна 180 градусов
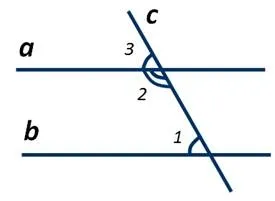
На рисунке видно, что a — \(\perp\) c, а b — \(\perp\) c. Поэтому из этого множества точек следует, что a\(\perp\) — это b.
Предположим, что a \(\perp\) c и b \(\perp\) c, но a не является \(\vert\) b. Тогда a и b пересекаются в некоторой точке. Рассмотрим треугольник ABC. Сумма углов равна 180º+∠C. Но этого не может быть. Значит, наша гипотеза ложна, и a \vert b.
Если обе прямые параллельны третьей
Далее следует доказательство теоремы из первой части статьи.
На представленных рисунках архитектурные сооружения содержат параллельные линии. Использование параллельных прямых линий в строительстве способствует повышению прочности этих сооружений и придает им исключительную красоту, привлекательность и величие. Линии электропередач также намеренно прокладываются параллельно, чтобы избежать пересечения или соприкосновения друг с другом, что может привести к короткому замыканию, отключению электроэнергии и дефициту электроэнергии. Рельсы также укладываются на параллельные линии, чтобы поезд мог двигаться плавно.
В трехмерном пространстве прямые, параллельные третьей, параллельны друг с другом
В живописи параллельные линии изображаются сходящимися на одной линии или рядом с ней. Эта техника называется перспективой, которая возникает в результате иллюзии зрения. С расстояния параллельные линии выглядят как две сходящиеся линии.
Две прямые, перпендикулярные третьей, параллельны

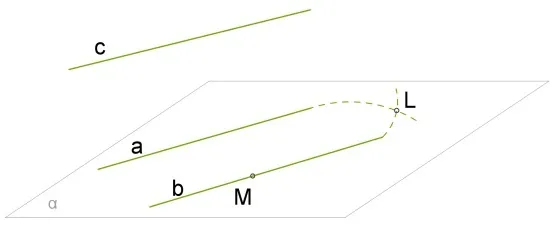
Доказательство параллельности прямых
- Есть a (прямая) и М (точка, далее — т.). Она не принадлежит a. Через них проходит плоскость альфа ( \(\alpha\) ). Известно, она единственная.Прямая b проходит через т.М и \(\vert\vert\;\) а. Она существует, что доказывает аксиома о \(\;\vert\vert.\)
- Предположим, что существует прямая с, которая тоже проходит через т.М, причем c \(\vert\vert\) a. В этом случае потребуется другая плоскость \(\beta\), такая, чтобы прошла через т.М. Такое невозможно, потому что есть теорема, которая говорит, что плоскость только одна. Значит это одна и та же плоскость ( \(\alpha\) совпала с \(\beta\) ) и одна и та же прямая (b совпал с c). Единственность прямой доказана.