Даже если вы не знаете определения, вы наверняка слышали о крысе, которая забегает за угол и разрезает его пополам. Это не заставит вас забыть, что такое биссектриса. А если вы не любите крыс, то с ними может столкнуться каждый. Дихотомус — это кошечка. Дихотомус — это лиса. Для воображения не существует правил. Все правила связаны с геометрией.
Равнобедренный треугольник: определение, теорема о свойстве высоты
Равнобедренный треугольник — это треугольник, у которого две стороны равны по длине.
Равные стороны называются боковыми сторонами, а третья сторона — основанием.
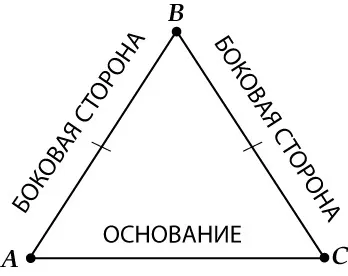
Признаки равнобедренного треугольника
- треугольник является равнобедренным, если два его угла равны;
- треугольник, в котором высота и медиана, высота и биссектриса, биссектриса и медиана, проведенные к одной стороне, совпадают, является равнобедренным, а эта сторона – основанием.
Свойство первое
В равнобедренном треугольнике углы при основании равны.
Внимание. Если учитель обнаружит плагиат в вашем сочинении, вам не избежать больших неприятностей (вплоть до исключения из школы). Если вы не можете написать эссе самостоятельно, закажите его здесь.
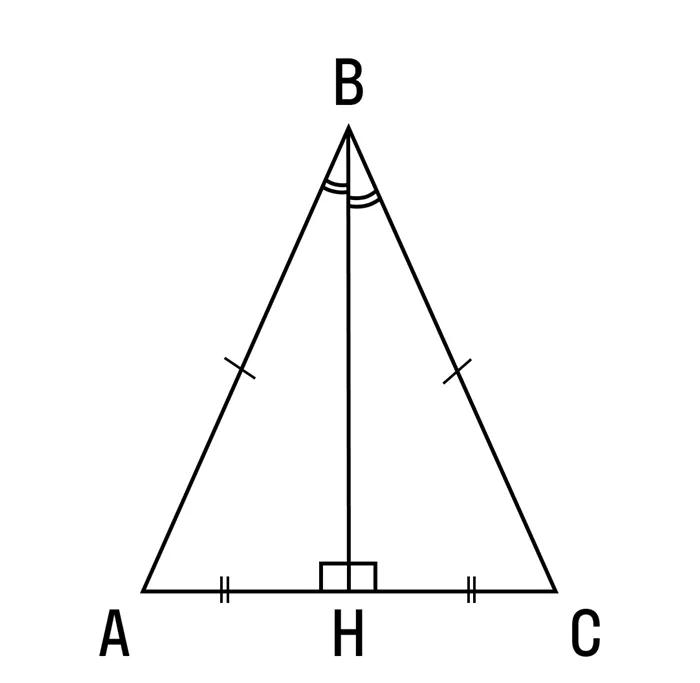
Дана равнобедренная фигура ΔABC, где AB = AC. Его основание имеет биссектрису угла AD.
Поскольку AD — биссектриса, угол ∠1 равен углу ∠2. Сторона AD является общей для ΔADB и ΔADC. Поэтому, исходя из первой характеристики, они равны. Тогда верно, что угол ∠B равен углу ∠C.
Свойство второе
В равнобедренном треугольнике биссектриса угла, лежащего на основании, является средней и высотой.
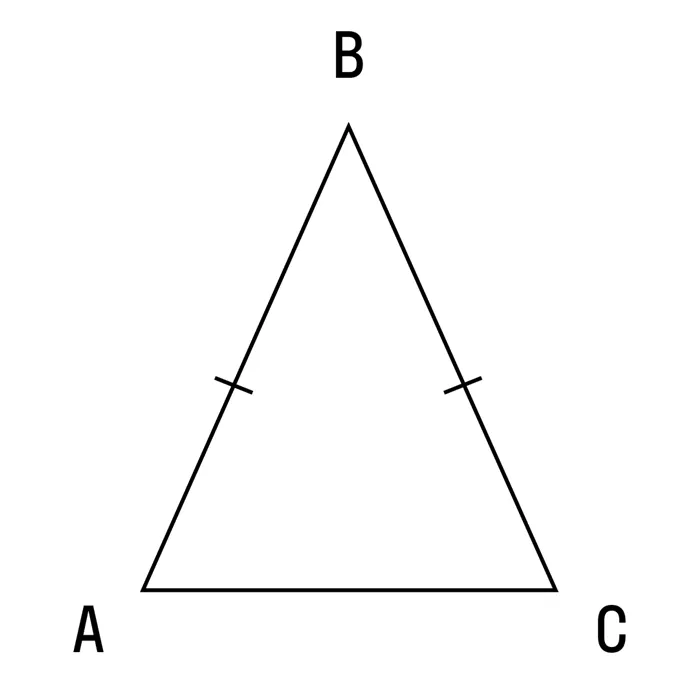
Дана равнобедренная фигура ΔABC, где AB = AC. Его основание имеет биссектрису угла AD.
Поскольку AD — биссектриса, угол ∠1 равен углу ∠2. Сторона AD является общей для ΔADB и ΔADC. Тогда эти треугольники равны первому знаку. Тогда BD = DC. Поэтому AD является медианой.
Сумма углов треугольника равна 180°, то есть ∠A + ∠B + ∠C = 180°. Поскольку AD — биссектриса угла, угол равен ∠A = 2*∠1.
В ΔACD ∠CDA + ∠1 + ∠2 = 180°, поэтому ∠CDA = 90°.
Затем AD — высота.
Свойство третье
В равнобедренном треугольнике медианы (или высоты и биссектрисы углов), проведенные из вершин к основанию, равны.
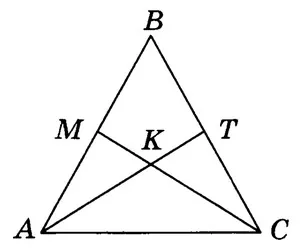
Дана равнобедренная фигура ΔABC с AB = AC.
∠BAT = ∠BCM, так как AT и MC — биссектрисы равных углов. ∠B является общим для ΔABT и ΔCBM; поэтому ΔABT и ΔCBM равны со вторым знаком. Тогда AT = CM.
Свойства равнобедренного треугольника: теория и задача
В этой статье мы рассмотрим определение и свойства равнобедренного треугольника. Мы также рассмотрим пример решения для закрепления теоретического материала.
Равнобедренный треугольник — это треугольник, у которого две стороны равны по длине (называются сторонами). Оставшаяся третья сторона — это основание фигуры.
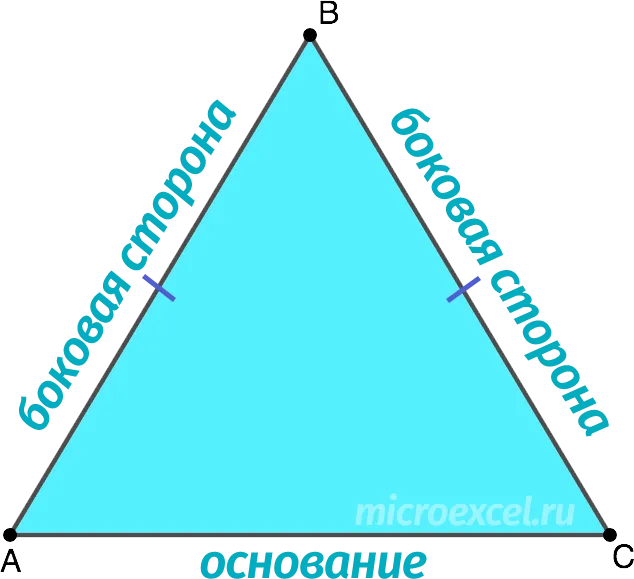
Свойства равнобедренного треугольника
Свойство 1
В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны. Это означает, что a = b.
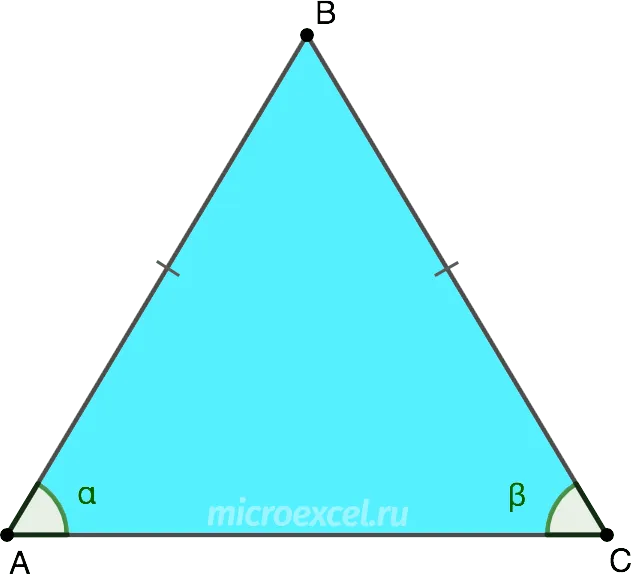
Если углы при основании треугольника равны, то это равнобедренный треугольник.
Свойство 2
В равнобедренном треугольнике высота, приходящаяся на основание, является одновременно биссектрисой угла и медианной плоскостью, простирающейся до
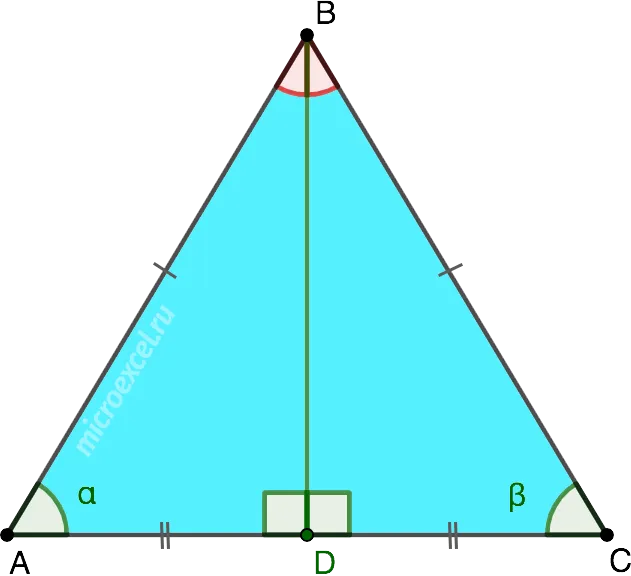
Теорема 1: В равнобедренном треугольнике углы при основании равны.
Свойство 3
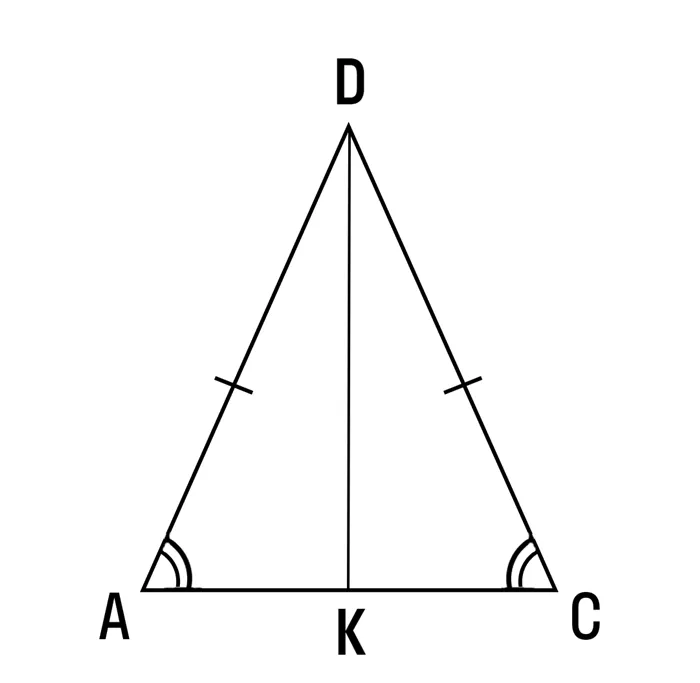
Пусть AC — основание равнобедренного треугольника. Начертите биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует, что все соответствующие элементы равны, поэтому угол A равен углу C. Осторожно!
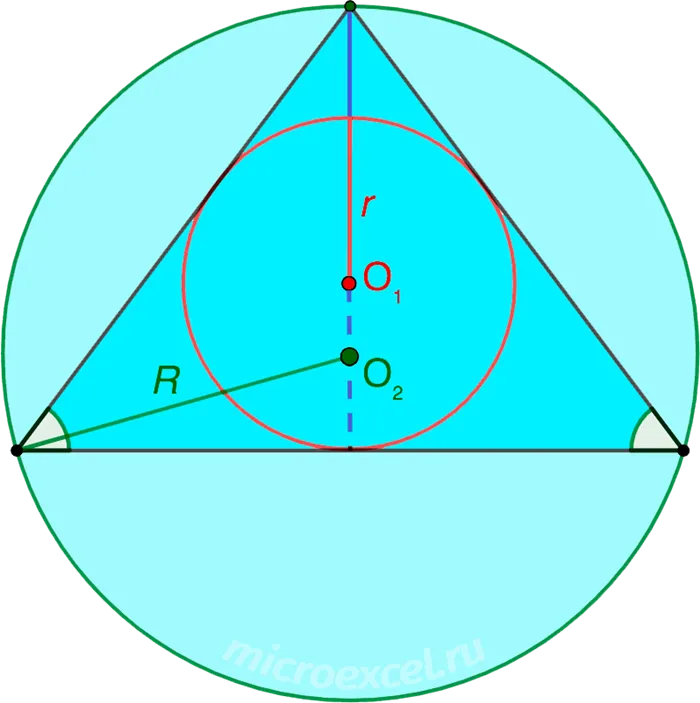
- O1Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является центром и высотой.2– расположены на одном отрезке;
- R – радиус описанной окружности;
- r – радиус вписанной окружности.
Пример задачи
Теорема 3: В равнобедренном треугольнике средняя линия, проведенная через основание, является биссектрисой угла и высотой.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой угла и медианой.
Занимайтесь по 15 минут в день. Освоить английскую грамматику и лексику. Сделайте язык частью своей жизни.
Нет ничего приятнее, чем упражняться в нахождении углов и сторон равнобедренного треугольника. Ну… почти ничего.
Публикации по теме:
- Нахождение площади квадрата: формула и примеры
- Нахождение площади прямоугольника: формула и пример
- Нахождение площади треугольника: формула и примеры
- Нахождение площади круга: формула и примеры
- Нахождение площади ромба: формула и примеры
- Нахождение площади трапеции: формула и примеры
- Нахождение площади параллелограмма: формула и примеры
- Нахождение площади эллипса: формула и пример
- Нахождение площади выпуклого четырехугольника: формула и пример
- Нахождение периметра квадрата: формула и задачи
- Нахождение периметра треугольника: формула и задачи
- Нахождение периметра прямоугольника: формула и задачи
- Нахождение периметра ромба: формула и задачи
- Нахождение периметра трапеции: формула и задачи
- Нахождение периметра параллелограмма: формула и задачи
- Нахождение длины окружности: формула и задачи
- Теорема косинусов для треугольника: формула и задачи
- Теорема синусов для треугольника: формула и задачи
- Теорема о сумме углов треугольника: формула и задачи
- Тригонометрические функции острого угла в прямоугольном треугольнике
- Нахождение объема цилиндра: формула и задачи
- Нахождение объема куба: формула и задачи
- Нахождение объема шара: формула и задачи
- Нахождение объема пирамиды: формула и задачи
- Нахождение площади правильного шестиугольника: формула и примеры
- Нахождение объема тетраэдра: формула и задачи
- Нахождение объема параллелепипеда: формула и задачи
- Нахождение площади поверхности куба: формула и задачи
- Нахождение площади поверхности цилиндра: формула и задачи
- Нахождение площади поверхности конуса: формула и задачи
- Нахождение площади поверхности вписанного в цилиндр шара
- Нахождение радиуса шара: формула и примеры
- Нахождение радиуса круга: формула и примеры
- Нахождение радиуса цилиндра: формула и примеры
- Нахождение площади прямоугольного параллелепипеда: формула и пример
- Нахождение площади правильной призмы: формула и задачи
- Нахождение площади правильной пирамиды: формулы
- Формула Герона для треугольника
- Теорема Менелая: формулировка и пример с решением
- Теорема о внешнем угле треугольника: формулировка и задачи
- Теорема Чевы: формулировка и пример с решением
- Теорема о трех перпендикулярах
- Теорема Фалеса: формулировка и пример решения задачи
- Геометрическая фигура: треугольник
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Свойства прямоугольного треугольника
- Свойства равностороннего треугольника: теория и пример задачи
- Определение и свойства медианы треугольника
- Определение и свойства медианы прямоугольного треугольника
Свойства равнобедренного треугольника
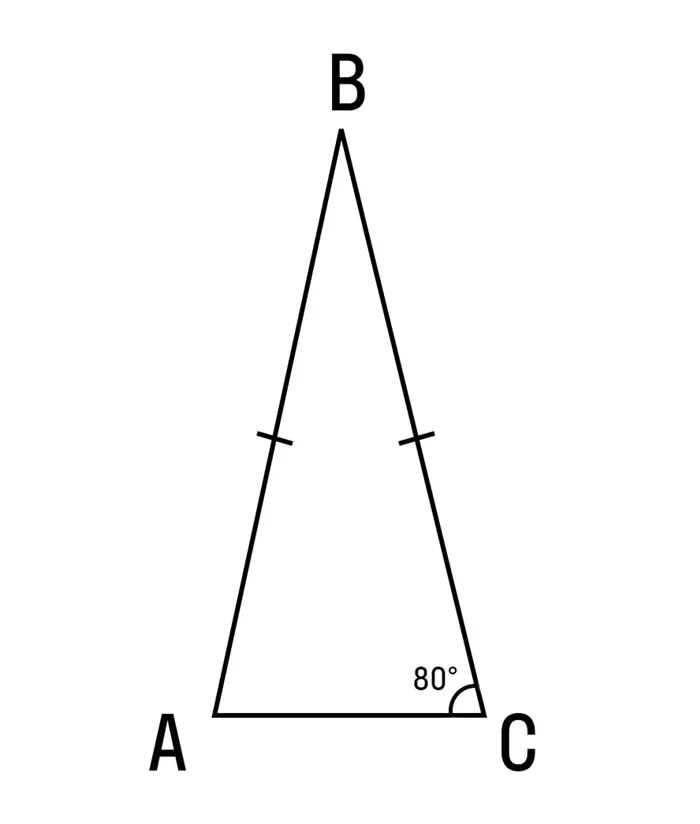
Первая проблема. Дано ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с несколькими теоремами, не секрет, что углы при основании равнобедренного треугольника равны, а треугольник ABC является равнобедренным, так как AB = BC.
Следовательно, ∠A = ∠C = 80°.
Вас также не должно удивлять, что сумма углов треугольника равна 180°.
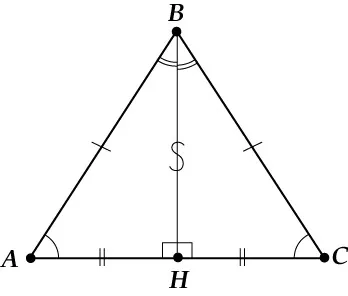
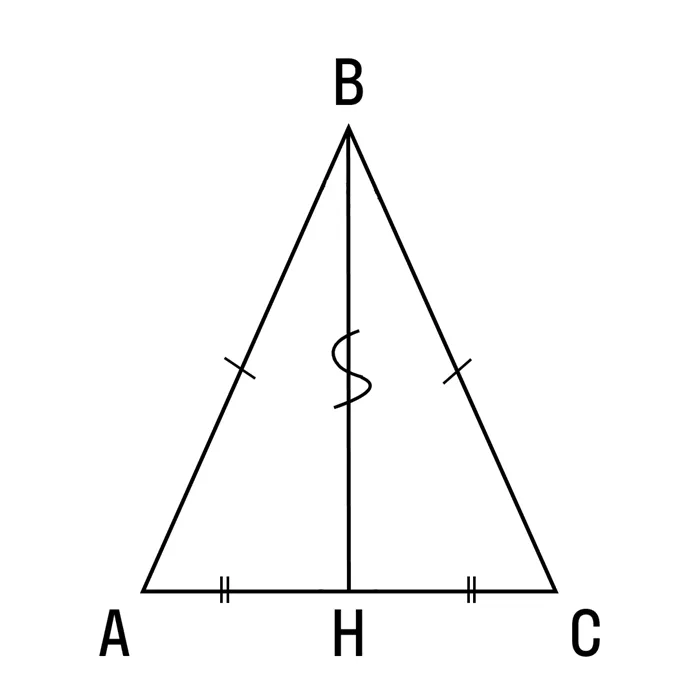
- Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
- Значит, во-первых, AH = HC и BH — медиана.
- Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.
∠B = 180° — 80° — 80° = 20°.
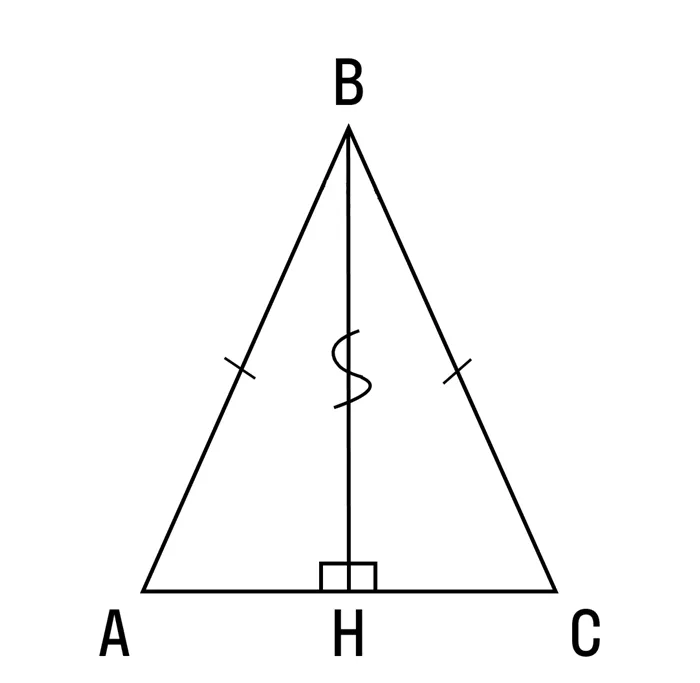
- Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
- Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
- Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Проблема вторая. Найдите высоту BH в треугольнике ABC, угол CAB равен 50°, а угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.
- Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
- Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
- Во-вторых, AH = HC и BH — медиана.
Лучший способ изучить свойства и точки равнобедренного треугольника — брать уроки математики с опытными репетиторами в Skysmart.

Примеры решения задач
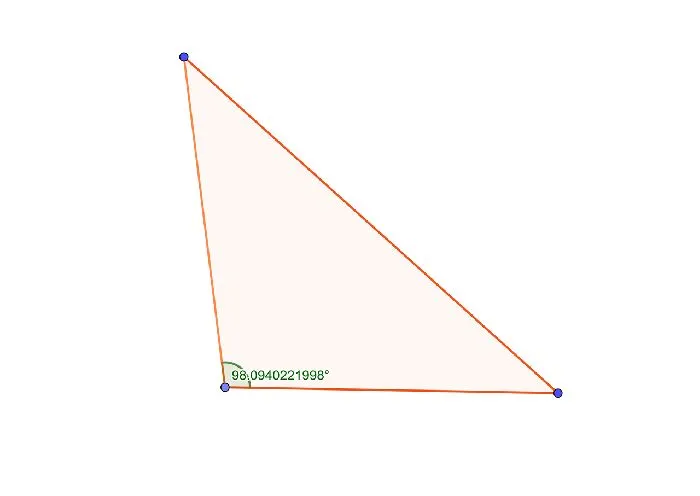
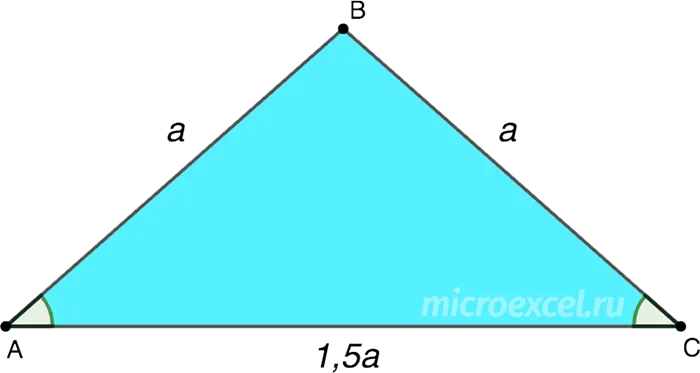
Равнобедренный треугольник — это треугольник с тупым углом на одной стороне и двумя равными сторонами на другой.
Такой равнобедренный треугольник трудно воспринимать визуально. Проблема в том, что студенты часто изображают тупоугольные треугольники с одной стороной так, что тупой угол находится при основании.
Однако, когда тупой угол нарисован у основания, фактическое основание тупоугольного равнобедренного треугольника визуально совпадает с боковой стороной. Такой подход очень часто приводит к ошибкам. Поэтому лучше начертить равнобедренный тупоугольный треугольник с тупым углом напротив основания и обозначить сам угол непосредственно на чертеже.
С другой стороны, такой подход не всегда помогает точно воспринимать фигуру как тупоугольный треугольник. По этой причине необходимо подписать углы и при решении доказать или проверить условие доказательства существования тупого угла в треугольнике.
- Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
- А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
- Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.
Равнобедренный тупоугольный треугольник