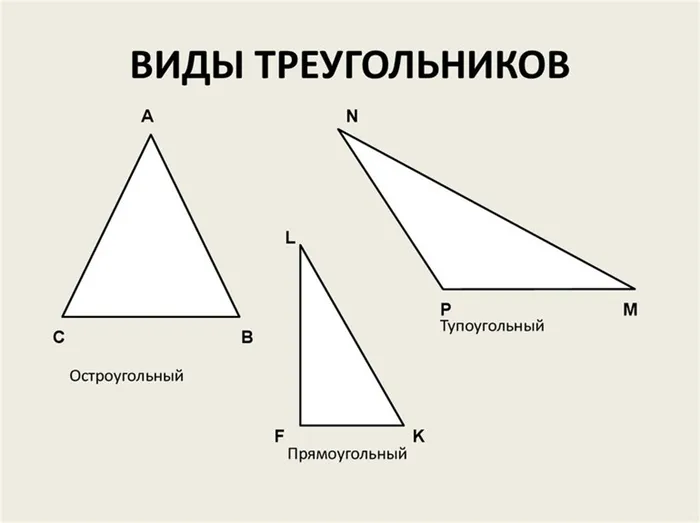
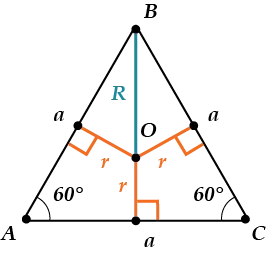Тупоугольный треугольник содержит тупой угол. То есть угол более 90 градусов. Два других угла в таком треугольнике острые.
Равносторонний треугольник, свойства, признаки и формулы

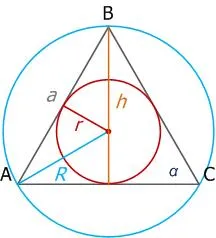
Равносторонний треугольник — это треугольник, у которого все стороны одинаковой длины и все углы одинаковой величины (60°).
Равносторонний треугольник (понятие, определение):
Равносторонний треугольник — это треугольник, у которого все стороны одинаковой длины и все углы одинаковой величины (60°).
Равносторонний треугольник также называют правильным или равносторонним треугольником.
По определению, каждый прямоугольный (равнобедренный) треугольник также является равнобедренным, но не каждый равнобедренный треугольник является прямоугольным (равносторонним). Другими словами, правильный треугольник — это частный случай равнобедренного треугольника.
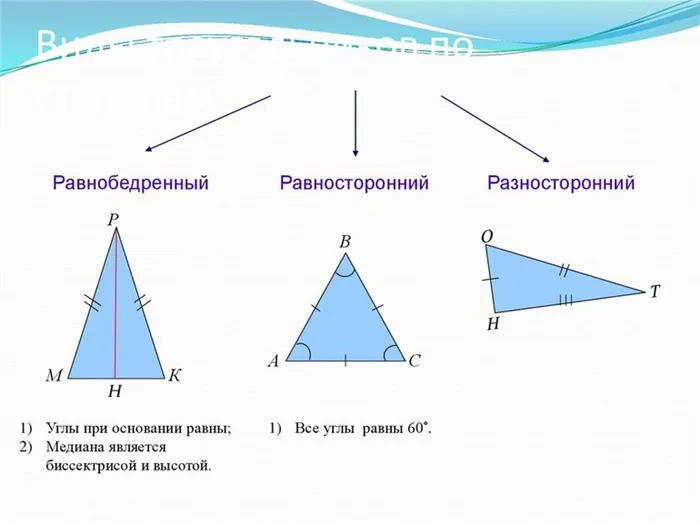
Рисунок 1: Равнобедренный треугольник
AB = BC = AC — стороны треугольника, ∠ ABC = ∠ BAC = ∠ AC = 60° — углы треугольника.
Свойства равностороннего треугольника:
1. в равностороннем треугольнике все стороны имеют одинаковую длину.
2. в равностороннем треугольнике углы равны и составляют 60°.
3. в равностороннем треугольнике каждая диагональ, проведенная к каждой стороне, является биссектрисой угла, а высота и равны друг другу.
В равностороннем треугольнике биссектриса угла, проведенная к каждой стороне, является средней линией, а высота и равны друг другу.
В равностороннем треугольнике высота, проведенная на каждой стороне, является биссектрисой угла, а средняя линия и равны друг другу.
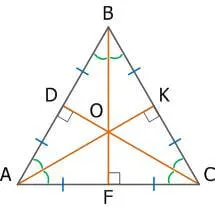
Рисунок 2. равнобедренный треугольник
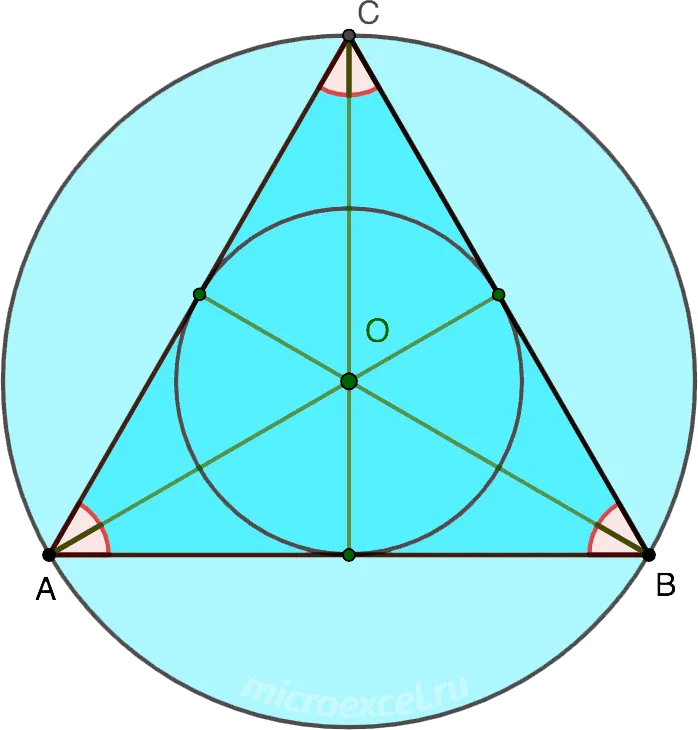
4. в равностороннем треугольнике высоты, биссектрисы углов, медианы и медианы пересекаются в точке, называемой центром равностороннего треугольника. Он также является центром эндоцикла и перицикла.
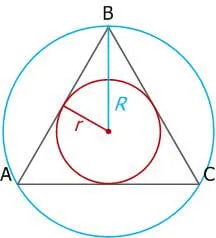
Рисунок 3. равнобедренный треугольник
R — радиус окружности, r — радиус эндо окружности.
5. радиус окружности равнобедренного треугольника в два раза больше радиуса эндокруга.
6. пересечение высот, биссектрис и медиан правильного треугольника делит каждую из них в соотношении 2:1, измеренном от вершин.

Рисунок 4. равнобедренный треугольник
AO : OK = BO : OA = CO : OD = 2 : 1
Определение равностороннего треугольника
Равносторонний (или прямоугольный) треугольник — это треугольник, у которого все стороны равны по длине. То есть, AB = BC = AC .
Примечание: Правильный многоугольник — это выпуклый многоугольник с равными сторонами и углами между ними.
Свойства равностороннего треугольника
Свойство 1
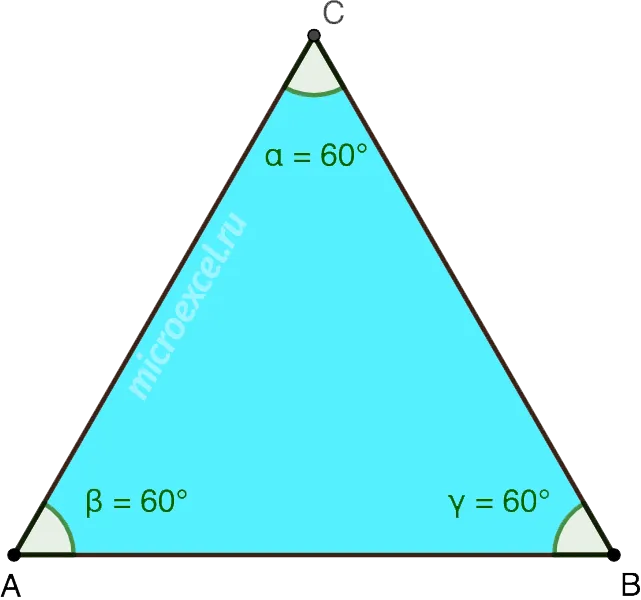
В равностороннем треугольнике все углы равны 60°. То есть, a = b = c = 60° .
Свойство 2
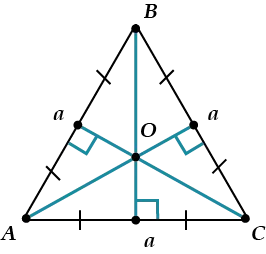
Высота равностороннего треугольника равна биссектрисе угла, из которого он образован, среднему и центру.
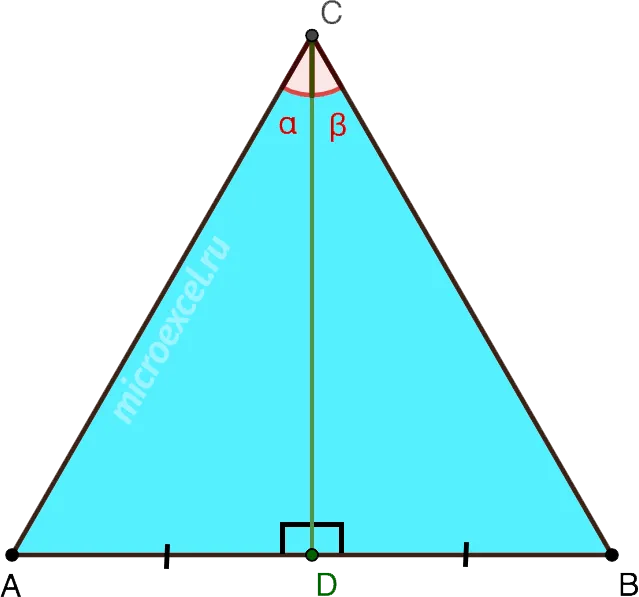
CD — медиана, высота и среднее значение AB и биссектриса угла ACB.
- CD перпендикулярна AB =>∠ADC = ∠BDC = 90°
- AD = DB
- ∠ACD = ∠DCB = 30°
Свойство 3
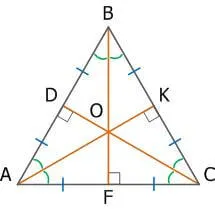
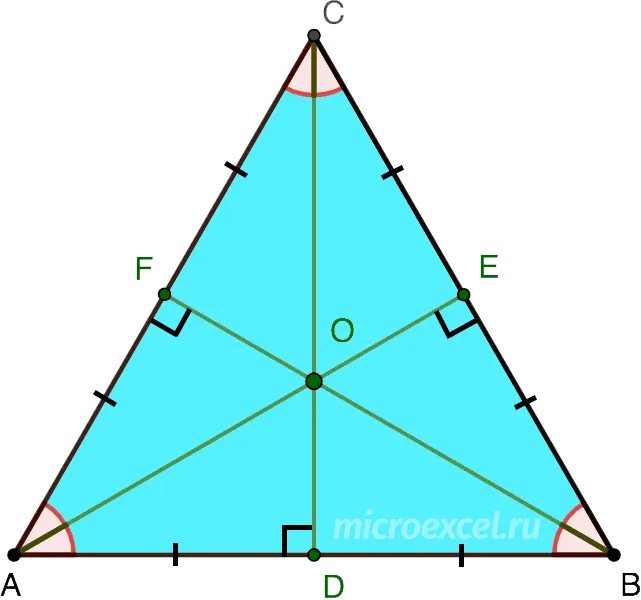
В равностороннем треугольнике биссектрисы, медианы, высоты и средние значения всех сторон пересекаются в одной точке.
Свойство 4
Центры акроокружности и окружности совпадают и пересекаются на пересечении медиан, высот, биссектрис углов и центров.
Свойство 5
Решение Примените формулы, приведенные выше, чтобы найти неизвестные величины:
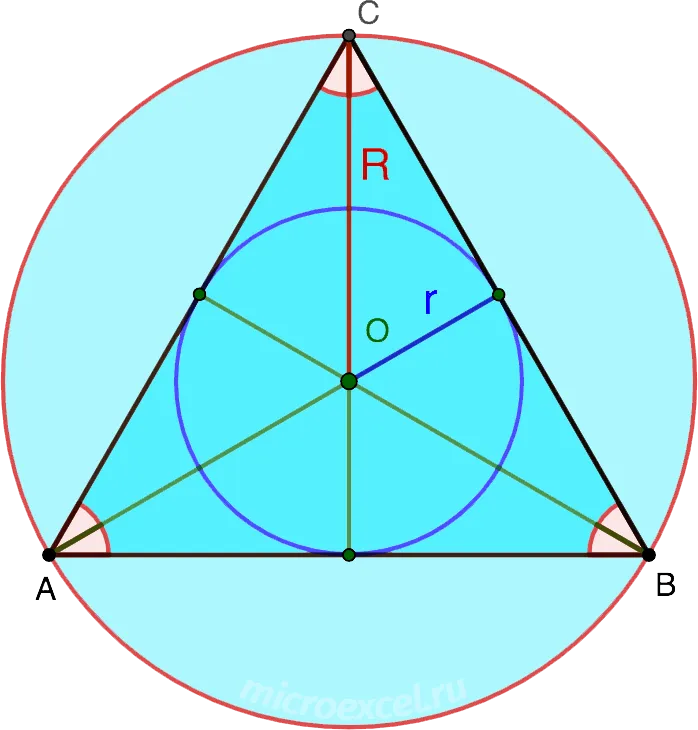
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r .
Свойство 6
Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и перпендикуляров совпадают — это одна и та же точка. Эта точка называется центром треугольника.
Почему? Рассмотрим равносторонний треугольник.
Он равнобедренный независимо от того, какая сторона взята за основание — он равнобедренный со всех сторон, так сказать.
Таким образом, каждая высота в равностороннем треугольнике также является биссектрисой угла, медианой и средним перпендикуляром!
В равностороннем треугольнике не \(12\) отдельных линий, как в обычном треугольнике, а только три!
Центр равностороннего треугольника — это центр конечной окружности и перикруга, а также пересечение высот и медиан.
Пример задачи
Свойство 3. В равностороннем треугольнике радиус перикруга в два раза больше радиуса конечного круга. \(R=2\cdot r\)
Теперь должно быть понятно, почему это так.
![]()
![]()
![]()
Публикации по теме:
- Нахождение площади квадрата: формула и примеры
- Нахождение площади прямоугольника: формула и пример
- Нахождение площади треугольника: формула и примеры
- Нахождение площади круга: формула и примеры
- Нахождение площади ромба: формула и примеры
- Нахождение площади трапеции: формула и примеры
- Нахождение площади параллелограмма: формула и примеры
- Нахождение площади эллипса: формула и пример
- Нахождение площади выпуклого четырехугольника: формула и пример
- Нахождение периметра квадрата: формула и задачи
- Нахождение периметра прямоугольника: формула и задачи
- Нахождение периметра ромба: формула и задачи
- Нахождение периметра трапеции: формула и задачи
- Нахождение периметра параллелограмма: формула и задачи
- Нахождение длины окружности: формула и задачи
- Теорема Пифагора для прямоугольного треугольника: формула и задачи
- Теорема косинусов для треугольника: формула и задачи
- Теорема о сумме углов треугольника: формула и задачи
- Тригонометрические функции острого угла в прямоугольном треугольнике
- Нахождение объема конуса: формула и задачи
- Нахождение объема куба: формула и задачи
- Нахождение объема шара: формула и задачи
- Нахождение объема пирамиды: формула и задачи
- Нахождение площади правильного шестиугольника: формула и примеры
- Нахождение объема тетраэдра: формула и задачи
- Нахождение объема призмы: формула и задачи
- Нахождение площади поверхности куба: формула и задачи
- Нахождение площади поверхности цилиндра: формула и задачи
- Нахождение площади поверхности конуса: формула и задачи
- Нахождение площади поверхности шара (сферы): формула и задачи
- Нахождение площади поверхности вписанного в цилиндр шара
- Нахождение радиуса шара: формула и примеры
- Нахождение радиуса круга: формула и примеры
- Нахождение радиуса цилиндра: формула и примеры
- Нахождение площади правильной призмы: формула и задачи
- Нахождение площади правильной пирамиды: формулы
- Формула Герона для треугольника
- Теорема Менелая: формулировка и пример с решением
- Теорема о внешнем угле треугольника: формулировка и задачи
- Теорема Чевы: формулировка и пример с решением
- Теорема Стюарта: формулировка и пример с решением
- Теорема о трех перпендикулярах
- Теорема Фалеса: формулировка и пример решения задачи
- Геометрическая фигура: треугольник
- Признаки равенства треугольников
- Признаки подобия треугольников
- Признаки равенства прямоугольных треугольников
- Свойства равнобедренного треугольника: теория и задача
- Определение и свойства медианы треугольника
- Определение и свойства медианы прямоугольного треугольника
Свойства равностороннего треугольника
Свойство 1. В равностороннем треугольнике все углы равны между собой и равны \(^>\)
Естественно, не правда ли? Три одинаковых угла, в сумме \(^>\), значит, каждый по \(^>\)
Рассмотрим рисунок: Точка\(O\) является центром треугольника.
Таким образом, \(OB\) — это радиус окружности (обозначается \(R\)), а \(OK\) — радиус эндоцикла (обозначается \(r\)).
Но точка \(O\) также является пересечением пространств! Напомним, что медианы делятся пересечением в соотношении \(2:1\), считая от вершины.
Поэтому \(OB=2\cdot OK\), т.е. \(R=2\cdot r\).
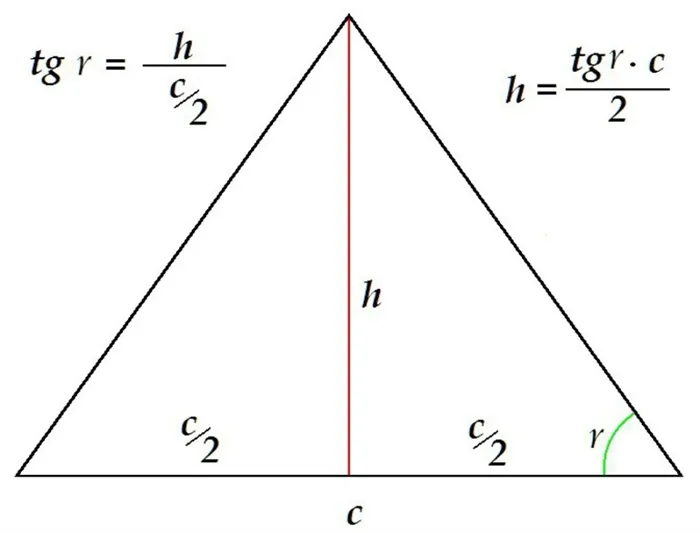
Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются длиной стороны.
Давайте убедимся в этом.
Это уже должно быть понятно:
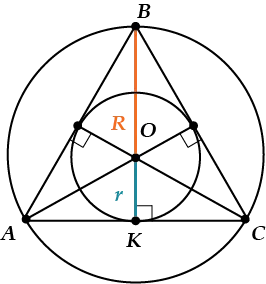
Мы постоянно работаем над улучшением этого учебника, и вы можете помочь нам. Доступ и неограниченное использование учебника Юклава (более 100 статей по всем темам ЕГЭ и ОГЭ, более 2000 решенных задач, более 20 вебинаров — практических занятий).
Радиус вписанной окружности равностороннего треугольника