Мы уже говорили о сокращении дробей. Мы выяснили, почему снижение возможно. Мы научились правильно сокращать. Мы привели алгоритм сокращения и два способа его выполнения. Мы рассмотрели пример сокращения дробей.
Сокращение обыкновенных дробей
В этом посте мы рассмотрим правило сокращения обыкновенных дробей, которое изучается в школьной алгебре в 6-8 классах. Мы также рассмотрим примеры решения проблем, чтобы улучшить ваше понимание и закрепить теоретический материал.
Когда числитель и знаменатель обыкновенной дроби имеют общий множитель, их можно разделить на этот множитель, получив новую дробь, которая будет равна исходной дроби. Это называется дробным сокращением.
Если числитель и знаменатель являются простыми числами друг друга, то дробь является несократимой.
Чтобы уменьшить фракцию, выполните следующие действия.
- раскладываем числитель и знаменатель на множители;
- зачеркиваем одинаковые числа, встречающиеся в обеих составных частях дроби;
- составляем новую дробь из оставшихся чисел.
Пример: Сократим дробь 27 /.45.
Решение Здесь мы имеем 9 как один из коэффициентов как числителя, так и знаменателя.
Сокращенная форма сокращения обычно записывается следующим образом: Числитель и знаменатель удаляются, подписывается коэффициент их деления с учетом общего множителя, затем добавляется знак равенства и записывается полученная дробь.
Сокращение может быть ступенчатым, т.е. дробь сначала делится на общий делитель, а затем на другой.
Использование НОД
Чтобы уменьшить дробь как можно больше за один раз, найдите наибольший общий делитель числителя и знаменателя. Затем нужно разделить только дроби на найденное значение.
Пример: Сократим дробь 564 /2448.
Решение Разложите числитель и знаменатель на простые множители.

Найдите число 2 дважды и число 3 один раз в обоих анализах. Следовательно, НОД (564, 2448) = 2 ⋅ 2 ⋅ 3 = 12 .
Таким образом, исходную дробь можно максимально уменьшить, разделив ее на 12.
Как сокращать дроби? Сокращение дроби до несократимого вида.
Чтобы получить несводимую дробь, нужно найти наибольший общий делитель (НОД) для числителя и знаменателя дроби.
Существует несколько способов найти НОД. В этом примере мы используем факторизацию с первым фактором.
Найдите несводимую дробь \(\frac\).
Решение. 48=2⋅2⋅2⋅2⋅3 136=2⋅2⋅2⋅2⋅2⋅17 NODES(48, 136)=2⋅2⋅2⋅2⋅2⋅2=6
Правило сокращения дроби до несократимого вида.
- Нужно найти наибольший общий делитель для числители и знаменателя.
- Нужно поделить числитель и знаменатель на наибольший общий делитель в результате деления получить несократимую дробь.
Пример: Уменьшить пропорцию \(\frac\).
Решение: Найдите NOD(152, 168). Разложим 152 и 168 на простые множители. 152=2⋅2⋅2⋅2⋅19=2⋅2⋅2⋅2⋅3⋅7 NODE(152, 168)=2⋅2⋅2⋅2⋅2⋅2=6
Реакция: \(\frac\) — несводимая дробь.
Сокращение смешанных дробей.
К смешанным дробям применяются те же правила, что и к обычным дробям. Разница лишь в том, что целую часть мы оставляем нетронутой, а дробную часть уменьшаем, или преобразуем смешанную дробь в неправильную, i
До каких чисел можно сократить дробь? Ответ: Дробь можно уменьшить на наибольший общий делитель или на общий делитель числителя и знаменателя. Например, дробь \(\frac\).
Давайте разделим числа 100 и 150 на простые коэффициенты. 100=2⋅2⋅5⋅5⋅5=2⋅5⋅3 Наибольший общий делитель равен НОД(100, 150)=2⋅5⋅5⋅5⋅5=50.
Получаем несводимую дробь \(\frac\).
Но не всегда нужно делить на NOD, можно также уменьшить дробь на простой делитель числителя и знаменателя. Например, 100 и 150 имеют общий делитель 2. Давайте уменьшим \(\frac\) на 2.
Получаем сокращающуюся фракцию \(\frac\).
Какие дроби можно сократить? Ответ: Вы можете сокращать дроби, у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac\). Числа 4 и 8 имеют число, на которое они оба делимы, а именно 2. Поэтому такую дробь можно уменьшить на число 2.
Пример: Сравните две дроби \(\frac\) и \(\frac\).
Эти две фракции одинаковы. Рассмотрим подробнее дробь \(\frac\):
Две дроби равны тогда и только тогда, когда одна из них получается в результате уменьшения другой дроби на общий множитель числителя и знаменателя.
Пример: Если возможно, сократите следующие дроби: a) \(\frac\) b) \(\frac\) c) \(\frac\) d) \(\frac\)
Обычное алгебраическое решение любой задачи сокращения дроби заключается в получении идентичной дроби, но в неполном виде. Чтобы получить несводимую дробь, ее делят на определенное число — наибольший общий делитель (сокращенно НОД):
Рассмотрим практическое использование дроби \frac
. Он может быть уменьшен на свой НОД, который равен 6. Тогда 6 : 6 = 1 и 12 : 6 = 2. Следовательно:
Последняя дробь является несводимой.
Обратите внимание, что в большинстве случаев, когда нам нужно сократить дробь, мы должны сделать это до получения несократимой дроби.
You may also like:

Что такое уравнение и корни уравнения? Как решить уравнение?

Деление рациональных чисел примеры и правила.

Нужен репетитор по математике (алгебре) или геометрии?
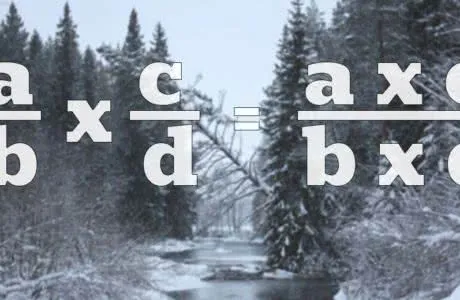
Как привести дробь к несократимому виду
Для примера возьмем дробь 144192. Сначала найдем наибольший общий делитель 144 и 192. Для этого можно воспользоваться методом простой факторизации:
144 : 2 = 72 192 : 2 = 96<6><12>72 : 2 = 36 96 : 2 = 48
36 : 2 = 18 48 : 2 = 24
18 : 2 = 9 24 : 2 = 12
Как сократить большую дробь
- следует найти наибольшее число, на которое делятся одновременно числитель и знаменатель;
- разделить числитель и знаменатель на это число.
9 : 3 = 3 12 : 2 = 6
3 : 3 = 1 6 : 2 = 3
Тогда наибольший общий множитель этих чисел равен 48 = 3 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2.
Разделите исходную дробь на 48, чтобы получить несократимую дробь:
Рассмотрим другой способ уменьшения числителя и знаменателя дроби на делитель, который легко определить с помощью простых математических символов. Если мы хотим уменьшить дробь типа 40008,800, мы сразу можем сказать, что существует общий множитель 100, который можно заключить в скобки:
Невооруженным глазом видно, что оба числа делятся на 2, результат снова делится на 2, и так далее. В итоге получается несводимая дробь \frac
= \frac
. Теперь мы можем сказать, что наибольший общий делитель дроби равен 800.
Если знаменатель дроби равен квадрату числителя, то такая дробь в несократимой форме всегда имеет вид: 1 в числителе + число в знаменателе, которое было числителем до сокращения:
Сокращение дробей — довольно сложная тема для 6 класса, поэтому к ней следует подходить постепенно. Чтобы избежать ошибок, лучше всего выполнять первые разрезы шаг за шагом одним и тем же способом. Здесь вы найдете алгоритм, который поможет вам избежать ошибок и научиться быстро и легко сокращать любые дроби.
Первое, что следует сказать, это то, что само сокращение дробей возможно благодаря одному из определений дробей.<5><11>Дробь — это неполная операция деления. Это означает, что любую дробь всегда можно заменить на коэффициент. Подстановка дробей необходима для точности вычислений.<4000><8800>Давайте на примере посмотрим, как выглядит замена дробей:
Чтобы не переписывать выражение каждый раз, мы можем использовать правило сокращения дробей: Если мы умножим или разделим знаменатель на одно и то же число, значение дроби не изменится.
Сокращение дробей

Теперь давайте напишем алгоритм. Чтобы уменьшить дробь, нам нужно:
Алгоритм сокращения дробей.
Вместо того чтобы записывать числитель и знаменатель в виде множителей, можно просто найти НОД числителя и знаменателя. Это максимально возможное число, на которое можно разделить два значения.
Специальной формулы для сокращения дробей не существует, но вы можете применять правила, приведенные в этом алгоритме.
Вот пример сокращения дробей. Для этого упростите дробь $
$. Мы намеренно выбрали большие числа, чтобы показать, как большее число может превратиться в маленькое путем упрощения.
Мы не ищем НОД, а делим числа на простые коэффициенты и находим суммарные значения.
- Представить числитель и знаменатель в виде простых множителей.
- Сократить каждый из равных простых множителей.
- Перемножить оставшиеся числа и записать результат.
513216:2=256608 — число в основном делится на 2. Чтобы число делилось на два, количество единиц должно быть четным.
256608:2=128304 — деление на 2 продолжается до того момента, когда последняя цифра числа перестает быть четной. Затем попробуйте разделить число на 3 и другие простые числа. Все простые числа находятся в таблице простых чисел.
Пример
Запишем результат деления. Давайте проанализируем 145152 таким же образом.<513216\over<145152>>145152=2*2*2*2*2*2*3*3*7 — всего 8 чисел 2, 4 числа 3 и одно число 7.
В обоих числах нужно вычесть 6 чисел 2 и 4 числа 3. Запишите полученный числитель. Остались следующие номера: 2, 3 и 11.
Напишите знаменатель. В итоге мы получаем следующие цифры: 2, 2 и 7.
Сокращение дает дробь:
$ — при желании можно извлечь целочисленную часть. Однако, если в этом нет необходимости из-за задания, вы можете оставить ответ как есть.
$<99\over<28>>








