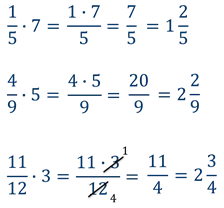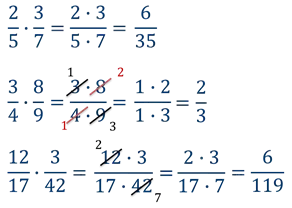Прежде чем начать перемножать числитель и знаменатель, необходимо проверить, можно ли сократить дробь. Если дробь можно сократить, вам будет легче продолжить вычисления.
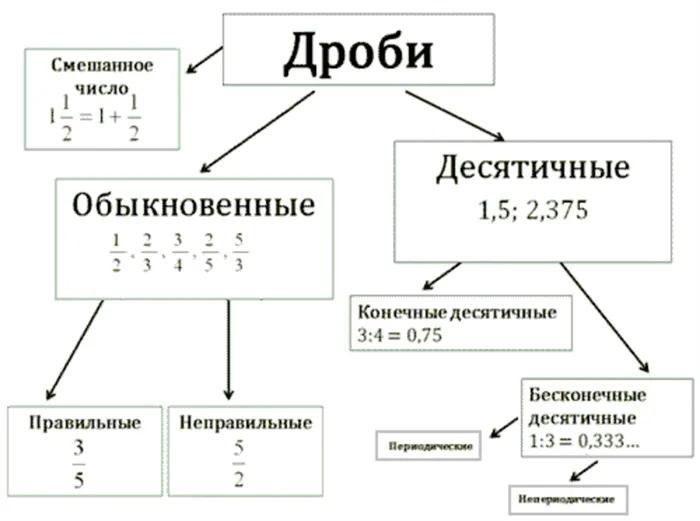
Как умножать смешанные дроби
Как умножить смешанную дробь на дробь, правило умножения смешанной дроби на обычную дробь, пример умножения смешанной дроби на обычную дробь и, наконец, как умножить смешанную дробь на обычную дробь с помощью калькулятора.
Правило умножения смешанных и нормальных дробей следующее:
Чтобы перемножить «смешанную и нормальную дробь», нужно преобразовать смешанную дробь в нормальную дробь и перемножить ее как нормальную дробь.
Чтобы запомнить правило умножения смешанных и обычных дробей, нам нужен пример, скажем, смешанная дробь 1|1/2. 1|1/2
и нормальная фракция.
А затем у нас есть пример умножения смешанных и обычных дробей!
1|1/2 * 1/5 Нам нет необходимости вдаваться в подробности — эти примеры просты, и мы уже много раз рассматривали подобные примеры в категории «Вычитание дробей». Набросаем алгоритм решения схематично:
Возьмем смешанную дробь — 1|2/3 и преобразуем ее в обычную дробь = 5/3. Получаем 5/3 умножить на 1/5, что является частным случаем умножения дробей: 5/3 * 1/5 = 5 : 5 /3 * 1/5 : 5 = 1/3 * 1/1 = 1/3 * 1 = 1/3 *1 = 1/3.
Как умножить смешанную и обычную дробь на калькуляторе!?
Чтобы перемножить смешанную и простую дробь на калькуляторе, не нужно знать никаких правил — достаточно знать, как вводить дроби на калькуляторе.
Нажмите многоцелевую клавишу — «*».
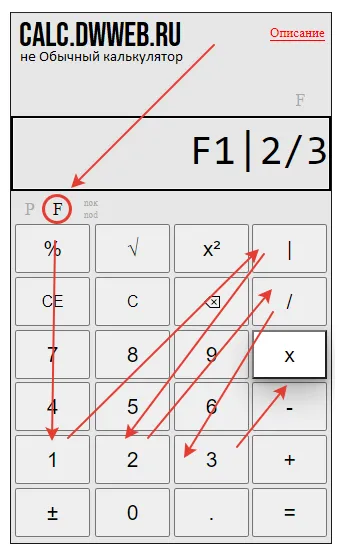
Введите дробь — 1/5.
Нажимаем кнопку равно — » https://dwweb.ru/__img/calc/a/0083_umnojit_smeshannuyu_na_obyichnuyu_drob_2020_09_21_10_03.png» alt=»Пример умножения смешанной дроби и обычной на калькуляторе.» title=»Пример умножения смешанной дроби и обычной на калькуляторе.»>
Результат умножения смешанной дроби на дробь мы получаем на калькуляторе:
Что такое смешанная дробь?
Смешанная дробь — это дробь, в которой подчеркнута целая дробь. Часто преобразование неправильной дроби в смешанную дробь выполняется после решения примера. Это хорошее эмпирическое правило: не оставляйте в результатах неправильную дробь.
Однако есть примеры, когда смешанные дроби нужно складывать, вычитать или даже умножать. Результаты таких примеров могут быть произвольными, поэтому не бойтесь делать собственные расчеты. При вычитании или умножении смешанных дробей могут получаться целые числа, дроби или смешанные числа.
Сложение и вычитание смешанных дробей
Сложение и вычитание смешанных дробей относительно просто:
- Выполняется действие над целой частью.
- Выполняется действие над дробной частью.
- Если при вычитании дробной части числа оказалось недостаточно, разрешается взять единицу у целой части.
- Если при сложении дробных частей получилась неправильная дробь, следует выделить целую часть и прибавить ее к сумме целых частей начальных дробей.
При преобразовании смешанных чисел в дроби и наоборот необходимо внимательно следить за цифрами. Помните, что потеря части числа может существенно повлиять на результат.
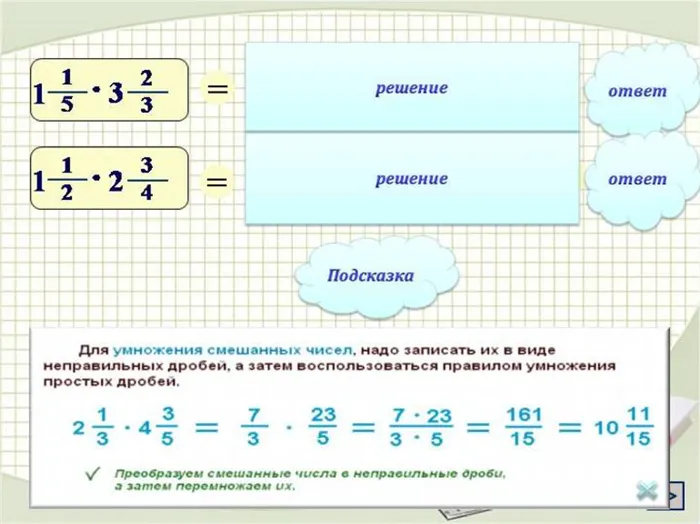
Умножение смешанных дробей
Умножение смешанных дробей сложнее. Во-первых, нельзя умножать отдельно целые и дробные части. Точно так же нельзя умножать дроби по отдельности.
Чтобы умножить смешанную дробь на другую смешанную дробь, необходимо сначала преобразовать их в неправильные дроби, а затем умножить их по правилу умножения обычных дробей.
Второй способ умножения дроби на число может быть более удобным.
Обратите внимание.
Деление дробей с участием натурального числа.
Чтобы умножить дробь на натуральное число, разделите знаменатель на это число, а числитель оставьте без изменения.
Из приведенного выше примера видно, что этот вариант лучше всего подходит, когда знаменатель дроби делится на натуральное число без остатка.
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.
В старших классах часто встречаются тройные дроби (или более). Пример:Чтобы перевести такую дробь в известную форму, используйте деление с двумя точками:

Второй способ умножения дроби на натуральное число.
Обратите внимание.
В старших классах часто встречаются тройные дроби (или более). Пример:Например, обратите внимание:
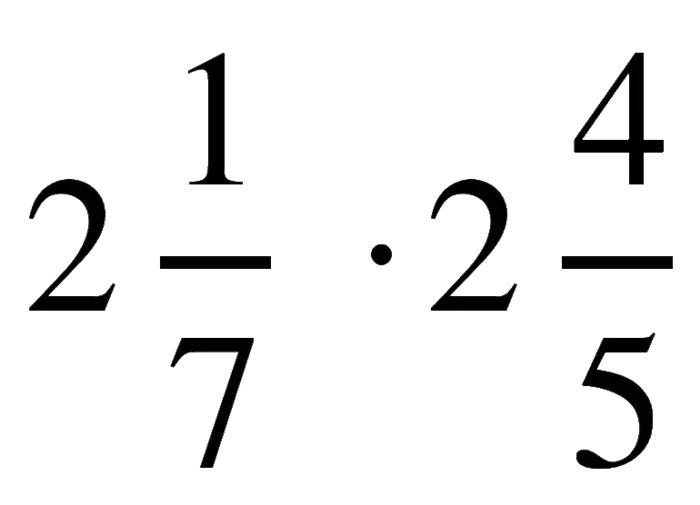
Если разделить единицу на любую дробь, результатом будет та же дробь, только в обратном порядке:
Многоэтажные дроби.
Практические советы по умножению и делению дробей:
1. Самое важное при работе с дробями — точность и внимательность. Выполняйте все расчеты тщательно и четко, с концентрацией и ясностью. Лучше написать несколько лишних строк на черновике, чем запутаться в расчетах в голове.
В старших классах часто встречаются тройные дроби (или более). Пример:3. сокращайте все дроби до тех пор, пока они не перестанут сокращаться.
4. полимерные дробные выражения должны быть преобразованы в обычную дробную форму путем деления на 2 балла.
5. Мысленно мы делим единицу на дробь, просто перевернув дробь.
На этом уроке мы разберем умножение дробей. Мы выведем правило умножения дробей на число, правило умножения дробей на дробь и правило умножения смешанных чисел. Применяйте эти правила при решении примеров.
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам необходимо добавить его в свой личный шкафчик.
2. Распространите видеоуроки среди своих учеников в личных кабинетах.
В этом уроке мы узнаем, как умножать простые дроби. Мы проработаем правила умножения дробей на натуральные числа, умножения дробей на обыкновенные дроби и умножения смешанных чисел.
Проблема
Маленький кот Васька ел сосиски на завтрак и ужин
Умножение дробей
Из этого обозначения легко понять, что числитель умножается на натуральное число, а знаменатель — на то же самое.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Запишем правило умножения дробей на натуральное число:


A br
3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Умножение дробей»