Все эти теоремы еще предстоит доказать в школе. Поэтому мы решили не проводить длительных математических и геометрических расчетов. Просто примите это как должное!
Трапеция – это стол, который стал геометрической фигурой
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы решили подробно поговорить о такой геометрической фигуре, как ТРАПЕ.

Она подробно рассматривается на уроках геометрии в 8 классе. И эти уроки являются частью общего знакомства учащихся с различными четырехугольниками.
Определение трапеции
Трапеция — это геометрическая фигура, представляющая собой четырехугольник с двумя противоположными сторонами на параллельных прямых линиях. Две другие стороны, с другой стороны, не должны быть параллельными.
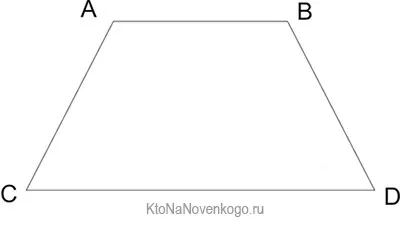
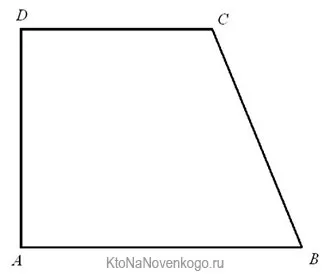
Вот как выглядит классическая трапеция:
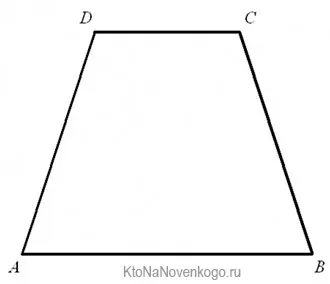
На этом рисунке стороны AB и CD параллельны. Но AD и CB не являются таковыми.
Происхождения слова
Первое упоминание об этой форме встречается в трудах знаменитого древнегреческого математика Евклида.
В его книге «Элементы» этим термином обозначается абсолютно любой четырехугольник, не являющийся параллелограммом.
Если вы не помните: параллелограмм — это четырехугольник, противоположные стороны которого параллельны. Эта форма в классическом смысле имеет следующий вид:
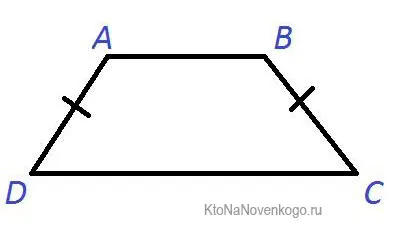
Интересно, что знакомые всем фигуры — квадрат, прямоугольник (что это?) и ромб (что это?) — также являются частным случаем параллелограмма. На самом деле — их противоположные стороны параллельны друг другу.
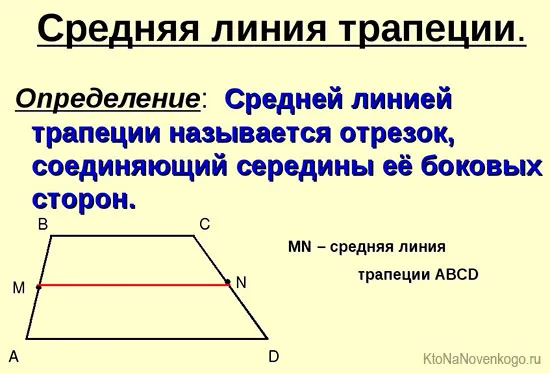
И оказывается, что Евклид был в целом прав. Он разделил все четырехугольники на две большие категории — параллелограммы и трапеции.
Кстати, слово ТРАПЕЦИЯ также греческого происхождения. В древности это звучало как «трапеция». В переводе это означает «обеденный стол». Отсюда же происходит слово «трапеза», которое мы используем как синоним любой еды.
Свойства трапеции
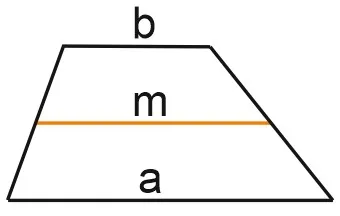
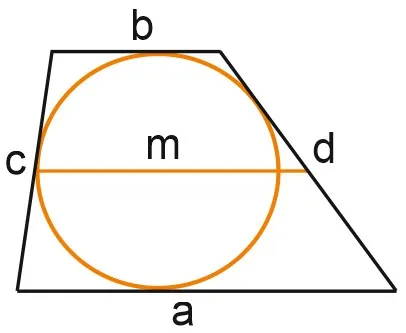
1. средняя линия трапеции параллельна основаниям и равна половине их суммы.
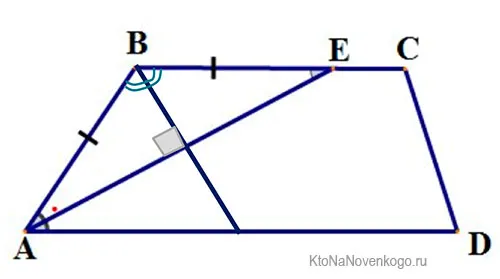
2. Биссектриса любого угла трапеции отсекает от ее основания (или продолжения) отрезок, равный боковой стороне.
Треугольники, образованные отрезками диагоналей и основаниями трапеции, подобны.
Отношение площадей этих треугольников равно .
4. треугольники и, образованные диагоналями и сторонами трапеции, имеют одинаковую площадь.
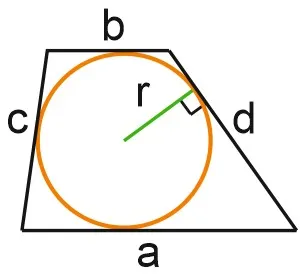
5. окружность можно вписать в трапецию, если сумма оснований трапеции равна сумме ее боковых сторон.
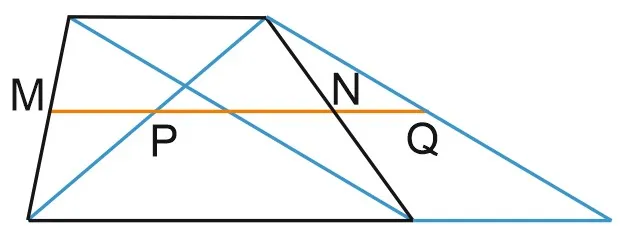
6. отрезок, соединяющий центры диагоналей, равен половине разности оснований и лежит на средней линии.
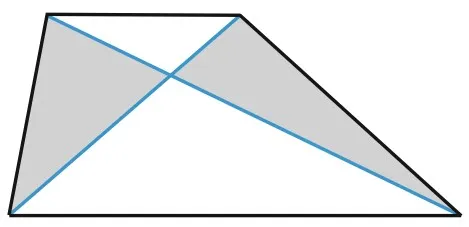
7. точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и центр оснований лежат на одной прямой.
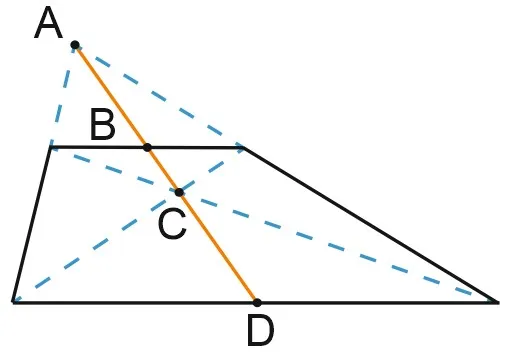
8. если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен половине их разности
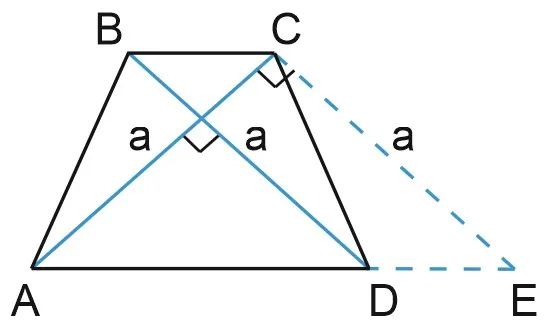
Свойства и признаки равнобедренной трапеции
Теорема 8: Площадь трапеции (как и любого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между диагоналями: где (вместо
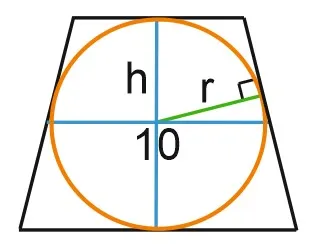
Теорема 9. Если круг можно вписать в трапецию, то (как и для любой окружности) площадь трапеции равна произведению ее полуокружности на радиус поперечной окружности:. таким образом.
Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравните эту теорему с теоремой 3).
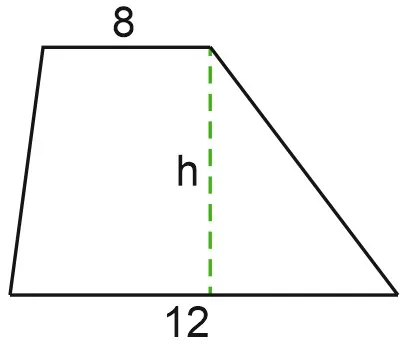
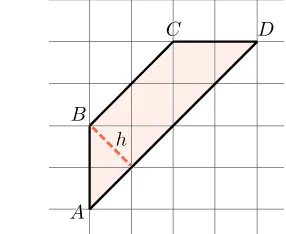
Найдите высоту трапеции ABCD, которая выпадает из вершины B, если стороны квадратных клеток равны.
Высота трапеции — это отрезок, перпендикулярный ее основанию. Начертите высоту от вершины. Если стороны квадратной клетки равны, то из теоремы Пифагора следует, что.
Площадь
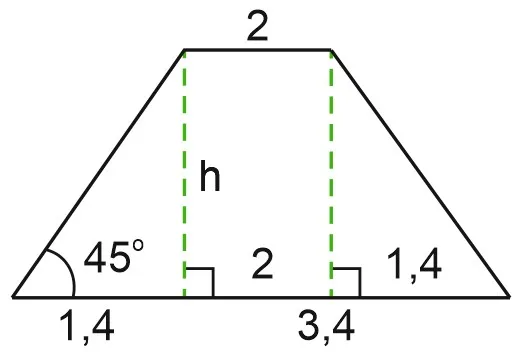
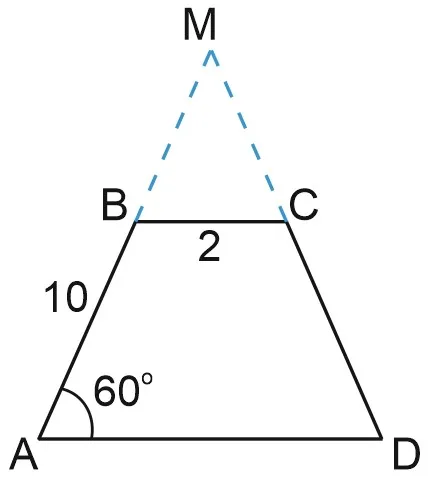
Основания стола равны 18 и 6, сторона, равная 7, образует угол с одним из оснований стола. Найдите площадь стола.
Углы ABC и BAH — косые, их сумма равна, и тогда BAH — это
Найдите высоту BH отрезка ABH. Поскольку половина гипотенузы равна отрезку, который находится под углом c, BH = 3,5.
- Графики тригонометрических функций. Синусоида
- Тригонометрический круг. Основные значения тригонометрических функций
- Площадь ортогональной проекции многоугольника
- Арифметическая прогресcия. Часть 1
- Тела вращения. Цилиндр
- Модуль. Раскрытие модуля. Простешие уравнения с модулем
Теоремы о площади трапеции
Площадь стола составляет .
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые диагональ делит среднюю линию этой трапеции.
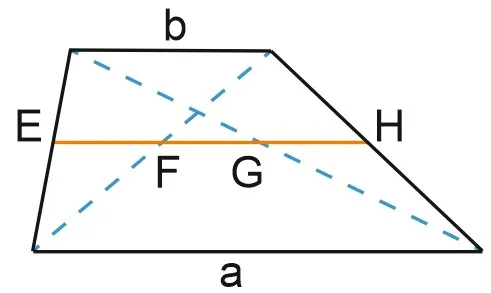
Что вы видите на рисунке? Вы можете сказать, что изображена трапеция ABCD и что у нее есть средняя линия. Но вы также можете увидеть два треугольника, ABC и ACD, с их средними линиями.
Помните, что средняя линия треугольника — это часть, соединяющая центры двух сторон. Средняя линия треугольника параллельна его третьей стороне и равна половине этой стороны. Из АКД видно, что
Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.
Задачи ЕГЭ и ОГЭ по теме: Трапеция
Начертите PQ, среднюю линию трапеции, PQ = 2,5 и. Из этого следует, что центр отрезка AC, PM, является средней линией треугольника ABC и PM = 1. Аналогично, NQ = 1.
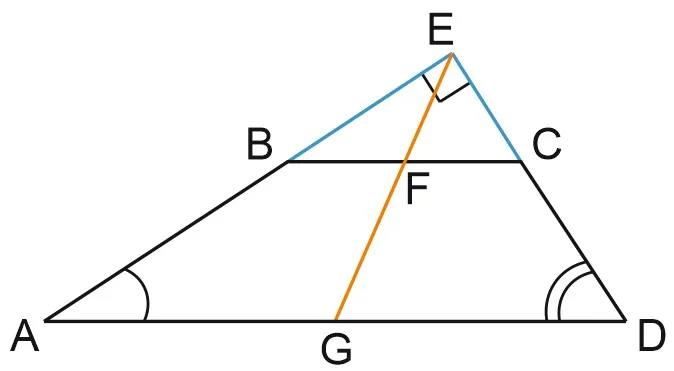
Прямая, проведенная параллельно боковой стороне трапеции через конец наименьшего основания, равный 4, пересекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
Периметр треугольника равен сумме его сторон, т.е.
Периметр трапеции равен
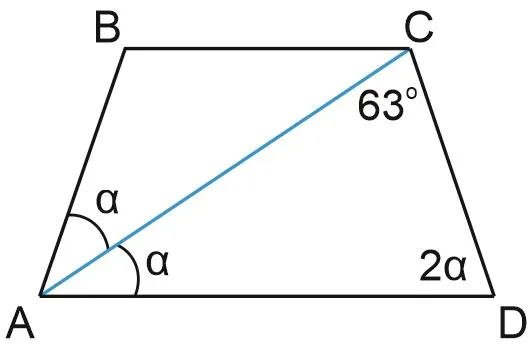
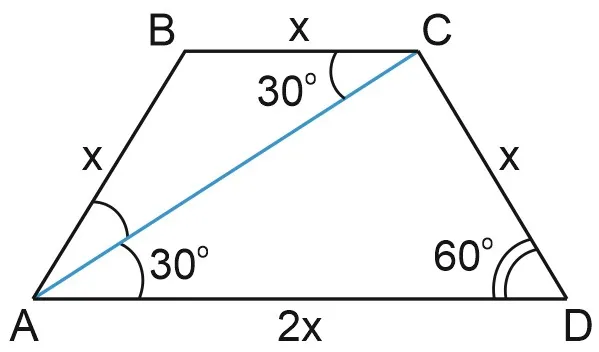
В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует угол со стороной CD. Определите углы трапеции.
Пусть CAD, тогда CAB и BAD, так как трапеция равнобедренная.
Сумма углов, таким образом
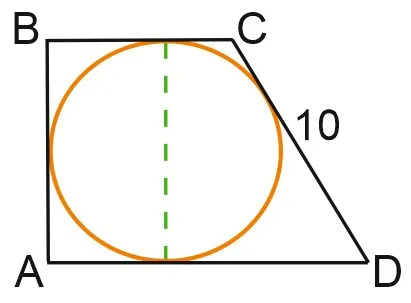
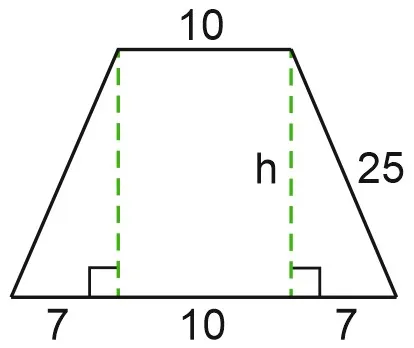
В равнобедренной трапеции основания равны 10 м и 24 м, а длина боковой стороны равна 25 м. Определите высоту трапеции.
Нарисуйте высоту
Начертите высоты DM и CN. Поскольку DM = CN и AD = BC, прямоугольники ADM и NCB равны гипотенузе и перпендикуляру (см. Правильный треугольник: свойства, доказательства равенства). Тогда \( \маленький \угольник A = \угольник B. \) Докажите далее, что \( \маленький \угольник ADC = \угольник DCB. \) \( \малый \угол A + \угол ADC=180° \), так как углы A и ADC являются односторонними углами, учитывая, что параллельные прямые AB и CD пересекаются прямой AD (Теорема 3 теорема об углах, образованных двумя параллельными прямыми и прямой). Аналогично \( \малый \угол B + \угол DCB=180°. \) Так как \( \малый \угол A= \угол B \), то \( \малый \угол ADC= \угол DCB. \)
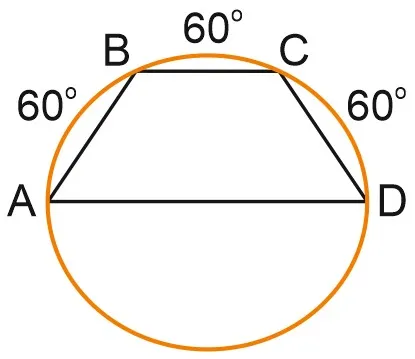
Собственность 2′. В равнобедренной трапеции диагонали равны.
Доказательство. Рассмотрим треугольники ADC и DCB (рисунок 12). У нас есть общая сторона CD и для обоих треугольников AD = CB, \( \маленький \ угол ADC=\ угол DCB. \) Тогда треугольники равны с двумя сторонами и углом между ними. Поэтому диагонали AC и DB трапеции ABCD равны.
Собственность 3′. Для равнобедренной трапеции высота, проведенная из вершины тупого угла к основанию трапеции, делит основание трапеции на части, большая из которых равна половине суммы оснований, а меньшая — половине разности оснований.
Доказательство. Рассмотрим четырехугольник DMNC (рисунок 11). У нас есть:
Тогда четырехугольник DMNC является прямоугольником. Так как треугольники ADM и NCB равны (см. доказательство вывода 1), AM = NB, значит DC = MN: