В математике существуют различные типы чисел. Одними из самых известных и часто используемых как профессиональными математиками, так и обычными людьми являются натуральные числа.
Натуральные числа | теория по математике 🎲 числа и вычисления
Определение Натуральные числа — это числа, используемые для подсчета предметов. Натуральные числа записываются с помощью 10 арабских цифр (0-9), которые составляют основу десятичной системы счисления, часто используемой для математических расчетов.
- Есть наименьшее число и нет наибольшего.
- Каждое следующее число больше предыдущего на 1 (исключение – сама единица).
- При стремлении к бесконечности числа растут неограниченно.
Иногда 0 также вставляется в ряд натуральных чисел. Это допустимо и называется расширенным натуральным рядом чисел.
Классы натуральных чисел
Каждая цифра натурального числа обозначает определенную цифру. Последняя цифра — это всегда количество единиц в числе, предыдущая цифра — количество десятков, третья сзади — количество сотен, четвертая — количество тысяч и так далее.
- в числе 276: 2 сотни, 7 десятков, 6 единиц
- в числе 1098: 1 тысяча, 9 десятков, 8 единиц; разряд сотен здесь отсутствует, поскольку выражен нулем.
Для больших и очень больших чисел можно увидеть устойчивую тенденцию (если смотреть на число справа налево, т.е. от последней цифры к первой):
- три последних цифры в числе – это единицы, десятки и сотни;
- три предыдущие – это единицы, десятки и сотни тысяч;
- три стоящие перед ними (т.е.7-я, 8-я и 9-я цифры числа, считая от конца) – это единицы, десятки и сотни миллионов и т.д.
То есть каждый раз мы имеем дело с тремя цифрами, обозначающими единицы, десятки и сотни более крупного номинала. Такие группы образуют классы. Если первые три класса более или менее часто встречаются в повседневной жизни, то остальные необходимо перечислить, поскольку не все знают их названия наизусть.
- 2-й класс – тысяча
- 3-й класс – миллион
- 4-й класс – миллиард (либо биллион);
- 5-й класс – триллион;
- 6-й класс – квадриллион;
- 7-й класс – квинтиллион;
- 8-й класс – секстиллион;
- 9-й класс – септиллион.
Сложение натуральных чисел
Сложение натуральных чисел — это арифметическая операция, в результате которой получается число, содержащее столько же единиц, сколько складываемых чисел.
Символом сложения является символ +. Складываемые числа называются слагаемыми, а результат — суммой. Пример:
Многозначные числа, которые трудно сложить в уме, обычно складываются в столбик. Для этого числа записываются одно под другим, выравниваясь по последней цифре, например, цифра единицы под цифрой единицы, цифра сотни под цифрой сотни и т.д. Если сложение цифр производится через запятую, то эта запятая записывается как единица над левой цифрой (т.е. за ней) и складывается с цифрами этой цифры.
Если в столбик складывается более 2 цифр, то в сумме цифр разряда может получиться превышение не на одну десятую, а на несколько десятых. В этом случае количество этих десятков переносится на следующий разряд.
Натуральные числа — это.
Натуральные числа — это числа, которые появляются, когда мы что-то считаем. Например: одно яблоко, два яблока, пять яблок, десять яблок и так далее.
Еще лучше притворяться, что считаешь людей, поскольку их нельзя разложить на части, как большинство предметов (например, разрезать яблоко пополам).

Само слово «naturalis» в переводе с латыни означает «естественный».
Однако если взять дроби (0,5, 13,856, 1/5 и так далее) и тем более отрицательные числа (-1, -5, -100), то в них мало естественности. Это означает, что можно дать другое, более простое определение натуральных чисел.
Если число не является ни дробным, ни отрицательным, его можно назвать натуральным числом.
Люди используют натуральные числа уже тысячи лет. Просто у разных народов были разные системы исчисления. Римляне, например, использовали палочки для счета. Так появились знаменитые римские цифры I, V, X, L, C, D и M.

В древнем Вавилоне, однако, использовалась шестнадцатеричная система. Эта система используется и сегодня в виде часов, где 1 час соответствует 60 минутам, а 1 минута — 60 секундам.
Наконец, современная символика цифр (0, 1, 2, 3, 4, 5 и т.д.) пришла от арабов, хотя они взяли за основу индийскую десятичную систему и добавили к ней «альфу».
Натуральный ряд
При сортировке натуральных чисел по возрастанию получается цепочка, называемая натуральным порядком.
Так всегда бывает, когда нам приходится считать что-то по частям. Например, в магазине мы обычно поступаем так с овощами или фруктами: покупаем 5 морковок или 3 яблока. И только потом мы их взвешиваем, потому что цены указаны за килограмм.

И конечно, таким образом, ученики учатся считать уже в первом классе. Например, если в задании пять флажков и вопрос: «Сколько?», то каждый ребенок считает «пальчиком», отмечает каждый флажок и слышит натуральное число: «один, два, три, четыре, пять».
Также важно знать, что количество натуральных чисел бесконечно. И поэтому последовательность натуральных чисел бесконечна.
Об этом говорится в основном законе натуральных чисел:
Каким бы большим ни было натуральное число N, всегда найдется натуральное число N+1, которое больше.
Ноль — это натуральное число или нет
Ряд натуральных чисел может быть построен двумя способами:
- из чисел, которые обозначают нумерацию предметов (первый, второй, третий, четвертый и так далее);
- из чисел, которые обозначают количество предметов (один, два, три, четыре и так далее).
Вы можете задаться вопросом, в чем разница? Во втором случае возможно, что нужного элемента вообще не существует. В этом случае количество элементов равно нулю.
То есть натуральное число начинается не с единицы, а с нуля. Это выглядит следующим образом: 0, 1, 2, 3, 4, 5 и так далее.

Поэтому в первом случае ноль не может считаться натуральным числом. Во втором случае — может. Интересно, что математики до сих пор расходятся во мнениях относительно того, какой подход является правильным. Сторонники обеих теорий примерно равны.
У российских студентов, однако, нет проблем с выбором. В нашей стране настаивают на версии, что ноль — натуральное число.
Натуральные числа. Ряд натуральных чисел.
История натуральных чисел уходит корнями в доисторические времена. Даже в древние времена люди измеряли вещи. Например, для торговли необходим подсчет товаров или для строительства — подсчет материалов. В повседневной жизни людям также приходилось измерять предметы, еду и животных. Первоначально числа использовались только для измерения в жизни, на практике, но позже, с развитием математики, они стали частью науки.
Натуральные числа — это числа, которые мы используем для измерения вещей.
Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …..
Ноль не относится к натуральным числам.
Все натуральные числа, или назовем набор натуральных чисел, обозначаются N.
Таблица натуральных чисел.
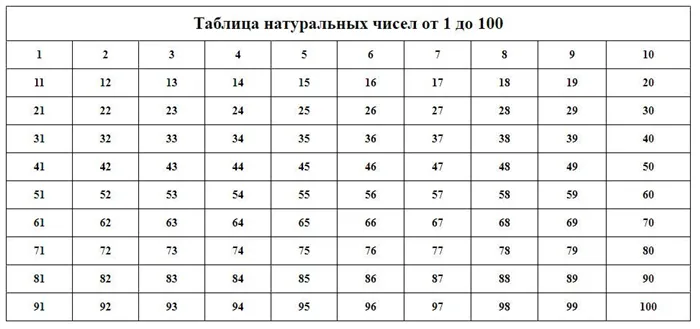
Натуральный ряд.
Натуральные числа, записанные в порядке возрастания, образуют линию натуральных чисел или набор натуральных чисел.
Пример № 7: На натуральной числовой прямой сколько чисел лежит между числами: а) 1 и 5, б) 14 и 19. Решение: а) 1, 2, 3, 4, 5 — три числа лежат между числами 1 и 5. б) 14, 15, 16, 17, 18, 19 — четыре числа лежат между числами 14 и 19.
- Наименьшее натуральное число – единица.
- У натурального ряда следующее число больше предыдущего на единицу. (1, 2, 3, …) Три точки или троеточие ставятся в том случае, если закончить последовательность чисел невозможно.
- Натуральный ряд не имеет наибольшего числа, он бесконечен.
Пример № 8: Назовите предыдущее число после числа 11. Ответ: 10.
Пример №9: Какие числа используются при подсчете предметов? Ответ: Натуральные числа.
Во-первых, мы установили, что 0 не относится к натуральным числам. Но естественно спросить: 10 — это натуральное число или нет? Конечно, это число и любое другое число с бесконечным числом нулей относятся к этому типу, потому что их можно использовать для счета или перечисления.
С натуральными числами можно выполнять различные математические операции.
Существует также степень натурального числа, которая обозначается так: ab, где: a — основание степени, b — экспонента. Например: 3 2 = 9.
Разряд — это место, где цифра расположена в числе. Каждая цифра названа индивидуально и расположена в порядке приоритета — справа налево и от низшего к высшему. Количество цифр в числе совпадает с количеством разрядов.
Младшая цифра равна единице, а старшая цифра всегда соответствует крайней левой цифре.
Например, число 5 469 состоит из четырех цифр:
Наибольшие цифры называются:
You may also like:

Десятичные дроби. Разряды и классы десятичных дробей.

Нужен репетитор по математике (алгебре) или геометрии?

Сравнение неправильных дробей правила и примеры.
Деление дробей. Правила. Примеры.
Натуральные числа с нолями
Цифры разделены на классы, каждый из которых содержит три цифры:
Действия, которые могут выполняться над натуральными числами
Для лучшей читабельности между классами принято ставить пробел.
- Сложение. Два или более чисел являются слагаемыми, а результат действия называется суммой: 345 + 1 813 = 2 158
- Вычитание. Первое число, называемое уменьшаемым, должно быть больше другого, которое именуют вычитаемым. В результате получаем разность: 455 — 120 = 335
- Умножение. Два или более множителей, а в результате получается произведение: 36 х 3 = 108
- Деление. Первое число, которое будет делиться, называют делимым, второе – делителем, а результат – частным. Может быть с остатком или без него: 450:15=30, 450:20=22 + остаток 10.
Что такое физические величины в математике? Это произвольные величины, выраженные цифрами ряда натуральных чисел. Другой пример: 184 345 567 100 — это число имеет четыре класса: Единицы, тысячи, миллионы и миллиарды.
Разряды и натуральные числа
- 9 – разряд единиц,
- 6 – разряд десятков,
- 4 – разряд сотен,
- 5 – разряд тысяч.
- десятки тысяч,
- сотни тысяч,
- миллионы и т. д,








